Том 4 (1999), No 3, сс. 15-23 |
19 |
| Точное решение задачи о колебаниях одномерной линии | |
|
|
Том 4 (1999), No 3, сс. 15-23 |
19 |
| Точное решение задачи о колебаниях одномерной линии | |
|
|
Проверим, как данные решения удовлетворяют моделирующей системе уравнений. Для этого достаточно проверить k–е и произвольное i-е уравнения системы (23). Подставим периодическое решение (24) в k-е уравнение системы (23). Для левой части получим: |
| (26) |
для правой части |
 |
(27) |
Следовательно, (24) удовлетворяет k-му уравнению системы. Теперь подставим (24) в i-е уравнение. В левой части получим |
| (28) |
в правой части |
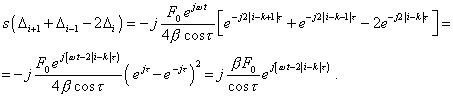 |
(29) |
Таким образом, периодическое решение полностью удовлетворяет системе уравнений (23). Теперь проверим апериодическое решение (25). Для левой части k-го уравнения имеем: |
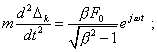 |
(30) |
для правой части |
 |
(31) |
Наконец, для i-го уравнения: для левой части |
 |
(32) |
и для правой части |
 |
(33) |
Таким образом, решения (24) и (25) полностью удовлетворяют моделирующей системе уравнений (23). Однако, как было сказано ранее, в отличие от решений для полубесконечной линии, в данной модели отсутствует конечное решение для критического режима. И это несложно доказать, подтвердив тем самым полноту комплекса решений (24)–(25). Согласно вышеуказанным
условиям критического режима, он является
промежуточным между периодическим и
апериодическим режимами; следовательно, если мы
в апериодическом решении устремим |
| (34) |
т.е. решения (24) и (25) полны так же, как и (6)–(8). Вместе с тем мы видим, что
решение для апериодического режима свободно
трансформируется в решение для критического, что
можно доказать и для связи между решениями для
периодического и апериодического режимов. В
сущности, все три полученных решения являются
тремя формами одного решения, которое
трансформируется в соответствии с величиной |