16

S.B. Karavashkin and O.N. Karavashkina

Кстати, на диаграмме, представленной на рис. 4, наглядно видно, что для одиночной пульсирующей сферы характер поля в ближней зоне является также прогрессивным и отличается от поля в дальней зоне только скоростью изменения его амплитуды с расстоянием. Таким образом, на основе существующего математического формализма никакой зоны стоячего поля не существует. Все попытки его обосновать - например, в [5] - основаны на некорректном приближении существующих уравнений для случая r << 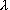. Данная некорректность отражается, в первую очередь, в пренебрежении пространственной фазой запаздывания процесса, по сравнению с временной характеристикой. Поскольку указанные члены являются аргументами тригонометрической функции, из мгновенной временной фазы процесса 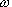  t может быть безболезненно изъято значение, равное целому числу периодов. Оставшаяся величина будет колебаться в пределах от 0 до 2. Следовательно, сколь бы близкое расстояние от источника мы ни брали, всегда можно найти интервалы времени, в которых временная фаза процесса будет меньше пространственной. Понятно, что это нарушает строгость неравенства r << 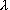., результат чего мы и наблюдаем на рис. 4. Хотя визуально динамика этого процесса может выглядеть обманчиво как стоячая волна вблизи излучателя из-за движения поверхности самой пульсирующей сферы. При суперпозиции нескольких источников ближняя зона будет образовываться и в ней будут прослеживаться процессы интерференции, которые мы теперь можем изучать на основе базы, наработанной в данном исследовании.

Выводы

В результате проведенного исследования установлено, что неконформное отображение полуполосы плоскости Zна равномерную радиальную метрику плоскости W наилучшим образом моделирует процессы в акустическом поле, создаваемом одиночной пульсирующей сферой.

На основе проведенного построения динамического неконформного отображения установлено, что при корректном применении существующего математического формализма стоячая волна в ближней зоне не возникает и все попытки её описания в области r << 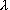являются следствием некорректного учёта взаимоотношения временной и пространственных фаз процесса в аргументе тригонометрической функции.

1. Каравашкин С.Б., Каравашкина О.Н.. Теоретическое обоснование и экспериментальное подтверждение существования поперечной акустической волны в газе,. SELF Transactions, 2 (2002), 1, с. 3- 16
2. Каравашкин С.Б., Каравашкина О.Н. Теорема о роторе потенциального вектора в динамических полях. SELF Transactions, 2 (2002), 2, с. 1- 9
3. Karavashkin, S.B. Some peculiarities of derivative of complex function with respect to complex variable. SELF Transactions, 1 (1994), pp. 77-95. Eney (Ukraine, in English).
4. Полякова А.Л. Акустический радиатор. Физический энциклопедический словарь, т. 1. Москва, Советская энциклопедия, 1960.
5. Doak, P.E. Noise and acoustic fatigue in aeronautics, An introduction to sound radiation and its sources. John Wiley & Sons Ltd., 1968.
6. Русаков И.Г. Импеданс акустический. Физический энциклопедический словарь, т. 2. Москва, Советская энциклопедия, 1962.
7. Корн Г.А., Корн Т.М. Математический справочник для ученых и инженеров. 720 с.
8. Лаврентьев М.А., Шабат Б.В. Методы теории функций комплексного переменного. Москва, Наука, 1973, 736 с.
9. Свешников А.Г., Тихонов А.Н. Теория функций комплексного переменного. - // Курс высшей математики и математической физики. Под ред. А.Н. Тихонова, В.А. Ильина и В.А. Свешникова. Москва, Наука, 1967.