SELF |
20 |
S.B. Karavashkin and O.N. Karavashkina |
|
|
|
SELF |
20 |
S.B. Karavashkin and O.N. Karavashkina |
|
|
|
The mathematical description reflects this phenomenology. The shown solutions (1) and (3) immediately follow from the construction in Fig. 1. Actually, if the beam passed from A to B during some time t and |
| (4) |
then on one hand |
| (5) |
hence |
| (6) |
On the other hand |
| (7) |
or, noting (6), |
| (8) |
Transforming (8), we yield (1) and from it yield (3). From this standard derivation we see that classical description of aberration is based namely on the finite time of beam passing along the section of measure, when the beam path coincided with each point of this section. This causes necessary an additional inclination of moving section of measure in relation to the beam trajectory. And though in the final formula the length of section is absent, the presence of this physical parameter makes valid the derivation for light aberration. So we neither phenomenologically nor practically may exclude the length of measurement section from the modelling of physical process of aberration. The fact that aberration is revealed in Galilean reference frame is not an evidence that the case of moving source and stationary observer is identical to the case of moving observer and stationary source. We can easily show it, considering the case of stationary observer and moving source of light, as shown in Fig. 3.
|
|
Fig. 3. The graph to calculate the classical effect of light aberration in case of distant source moving with some velocity vS relating to the stationary observer
|
As we can see from Fig. 3, having changed the phenomenology, we basically changed the statement of problem. Now we have not a difficulty in beam trajectory coincidence with the ruler AB, but the direction of beam S'B relates not to the real location of the source S at the moment of measurement, but to the location S' at an earlier moment, whose wavefront reaches the measurement section AB at the moment when we are measuring. When the model was changed, the modelling equations are changed, too. Now, if the beam arrived from S' to the point A during the time tS, with the source speed vS we yield |
| (9) |
Then, by analogy with the previous derivation, |
| (10) |
hence |
| (11) |
Proceeding from the obvious equality |
| (12) |
and using (9) and (11), we yield |
| (13) |
Comparing (13) with the related solution for the moving
observer (8), we can make sure that the solutions are not equivalent. It will be most
clear, if we pass to the angle |
or |
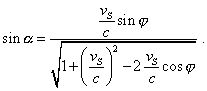 |
(14) |
Thus, on one hand, in both cases, the distance that beam
passed along the moving measurement ruler in one case and from the moving source to
stationary observer in another case, are eliminated from the final solution. With it the
value of aberration in both cases depends on ratio of observer’s either source’s
velocity to that of light. And the sign of angle |
| (15) |
But on the other hand, in case of moving observer, the
aberration angle depends on the source location indicated by the observer, while in case
of moving source this angle depends on the source location at the moment of indication.
Due to this, in the right part of (14) there appears the denominator, which depends both
on the velocity of source displacement and on the observation angle. With the observed
location of star at the zenith, i.e. with |
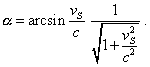 |
(16) |
We see from (16) that at small velocities of mutual approach of the source and receiver (i.e. when the speed v or vS was small in comparison with that of light), (3) and (16) give approximately same results for the star registered at the zenith, with accuracy to first order of relation of mutual speed of source and observer to that of light, |
| (17) |
But with growing speeds, (3) and (16) will basically differ, and at v or vS equal to the speed of light, we yield for the case of moving observer and stationary source, for the star registered at zenith, |
| (18) |
while in case of stationary observer and moving source, we in accordance with (16) have |
| (19) |
and can see, in this case the inclination angle (18) considerably differs from (19). But if the star is seen not at zenith, the difference is revealed also at small speeds, as in this case (17) comes to |
| (20) |
Thus, despite the cases of observer’s and source’s motion seem identical, the result generally is not identical. As was said above, the cause is that in this problem the observer compares the direction, in which the beam is registered with the direction of moving ruler, whose part in the first case takes the length of telescope tube, and in the second - the distance from the star to observer. Namely because in each of these cases the moving ruler is other, we yield different results. On the basis of this derivation we can clearly show the geometric cause of yielded non-identity. In Fig. 1, with moving observer, the beam of light received by the point B of the ruler passed ‘a short’ way AO, not a ‘long’ way AB. In case of source motion the beam registered by the point B (see Fig. 3) passes in its geometrical construction the ‘long’ way S'A, not ‘short’ way SA. With it, should in the second case the beam passed ‘short’ way SA, solutions would become fully identical. But the observer basically cannot see the beam emitted from the location S, as the wavefront from this location of source still has not reach the observer. This circumstance makes the considered variants non-identical. |
Contents: / 18 / 19 / 20 / 21 / 22 / 23 / 24 / 25 / 26 / 27 / 28 /