SELF |
26 |
S.B. Karavashkin and O.N. Karavashkina |
|
|
|
SELF |
26 |
S.B. Karavashkin and O.N. Karavashkina |
|
|
|
In this light, the methods allowing to determine simultaneously the incidence angle have an unquestionable advantage. And namely this circumstance was leading for Airy when he planned his experiment with the telescope filled with water, should the above-described masking effects of telescopic systems did not prevent him. At the same time, the masking effects prompt us the direction to improve our experimental method. The main here is to avoid any telescopic systems. In other words, we have to base our technique to measure the absolute angle of aberration on the scheme of quadrant shown in Fig. 9.
|
|
Fig. 9. Double quadrant to measure the absolute angle of aberration
|
This quadrant consists of two sight rulers with diopters, in one of them the ray between the diopters passes in the air, and in another - in the transparent material having a high refraction coefficient. These can be special kinds of glass either a fibre bundle. In this last case the bundle has to take a part of space between the diopters. In case when the space between the diopters was fully filled by the transparent material, the modelling equations which describe the measurements of this quadrant will fully correspond to the above model shown in Fig. 4. In particular, the relationship of inclination angles of sights will obey (29). The expression for the Earth speed calculation on the basis of (29) will be |
| (67) |
where |
| (68) |
and namely this difference will be directly measured by
the double quadrant - this means, this measurement will be most accurate. And the error of
observation angle From this method we see that the angle To determine this angle, we have to complicate the general scheme of measurement, as is shown in Fig. 10.
|
|
Fig. 10. The scheme to determine the angle
|
In this scheme we will use two identical measurements for
two stars S1 and S2; the observation angle
between them is strongly 90o. Each measurement we will make by the double quadrant in
relation to the arbitrarily chosen convenient for our measurement direction x'.
We will obtain two equations necessary to find the unknown angle |
| (69) |
and the second equation, accordingly, |
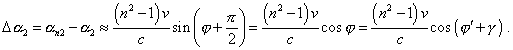 |
(70) |
The expressions (69) and (70) immediately account the circumstance that the basic relationship (67) has been written not for an arbitrarily chosen direction x', but for the direction of observer’s velocity x. On the grounds of this system of equations we will easily yield |
| (71) |
Thus, measuring the declination angles and differential angles of aberration for an arbitrarily chosen direction, we determine also the velocity of observer in the plane of measurements and the true direction of this velocity in the plane of observation. When we improved the method to measure by double quadrant, we see its advantages in comparison with the inversion speed method. They are the following. Firstly, we can simultaneously measure all parameters necessary to calculate the absolute angle of aberration. Secondly, the quadrant will measure immediately the difference of aberration angles of the sight rulers, which allows to achieve the utmost accuracy of calculation. And thirdly, the measurements are not referred to the Earth’s orbital plane, due to which the double quadrant can measure the absolute speed of the Earth in space, together with the Sun system and the Galaxy, irrespectively of the Earth orbital plane. And the main advantage of this method is a straight measurement of the calculation parameters without masking effects that blur the positive result in the interferometric methods which used Michelson, Morley, Miller, Kennedy and other researchers who sought the aethereal wind. The only what can diminish the value of measured speed is Miller’s possibly true premise that the Earth drags aether. But in this case also, the method of double measurement will enable to answer this complicated question. |
Contents: / 18 / 19 / 20 / 21 / 22 / 23 / 24 / 25 / 26 / 27 / 28 /