V.5 No 2 |
27 |
| On light aberration | |
|
|
V.5 No 2 |
27 |
| On light aberration | |
|
|
Speaking of possibility of non-interferometric measurements of the speed of absolute motion of observer free of considerable masking effects, which are inherent in interferometric methods, let us additionally consider the following conceptual experimental method. Truly speaking, it has no direct concern to the aberration effect. This method is based on the measurement of phases of emission of two frequencies emitted by the common emitter of microwave range. These frequencies pass simultaneously the common distance from the emitter 3 and receiver 4. To make it practically, we have to set the emitter and receiver onto some rigid underpinning able to turn by 360oaround its axis, as shown in Fig. 11.
|
|
Fig. 11. The scheme of the method to measure the phase difference: 1 is the generator, 2 is the receiver, 3 is the emitting antenna, and 4 is the receiving antenna
|
To describe this method mathematically, suppose, the emitter simultaneously emits two strongly monochromatic EM waves towards the receiver. The E-components of these waves we can write as |
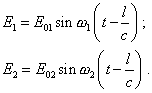 |
(72) |
These waves We see from (72) that the current time t is
common for both rays. The frequencies |
| (73) |
Thus, |
| (74) |
The further description of the method we will conveniently give, noting the particular features of classical and relativistic formalisms.
|
|
Fig. 12. The graph for calculation of delay of EM wave propagating along the moving measuring rod from the view of classical formalism
|
From the view of classical formalism, the calculation can be made on the basis of Fig. 12. From the graph, |
| (75) |
where |
| (76) |
At small velocities of the frame, we can approximately write (76) as follows: |
| (77) |
Noting that from the view of classical formalism the EM wave propagation speed is constant in relation to the aether, we can write |
| (78) |
or |
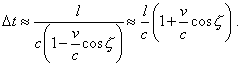 |
(79) |
Multiplying the right and left parts of (79) accordingly
by |
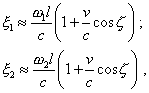 |
(80) |
and from (80) yield |
| (81) |
We see from (81) that the sought effect of the phase of two received signals depends on the first order of ratio v/c and can be regulated, if we change the difference of frequencies received by the receiver, and can be less changed by the size of base on which the emitter and receiver are fixed. To write mathematically the effect expected from the view of relativistic formalism, we can use the conclusions of basic relativistic theory, which states that the speed of light in the accompanying frame is strongly constant and the observer is unable to independently measure the difference in longitudinal and transverse sizes. With this approach, we will see no changes when the device turns. Thus, the described method allows to reveal and to experimentally study the effect of frame’s motion in relation to the aether. From the view of classical formalism, the phase difference has to change with the turn of device, describing some cardioid, as shown in Fig. 13. And this change of phase is the effect of first order of the ratio v/c, which, after relativistic opinion, cannot be realised in the experiments of such kind.
|
|
Fig. 13. The change of phase difference of received two-frequency signal plotted against the angle of device turn to the aethereal wind, according to classical formalism
|
We can regard as the advantage of suggested method the fact that errors of the system tuning will have no influence on the effect. The only stipulation is important for this method: the EM waves of both frequencies have to be emitted and received by one source and receiver having no focusing devices and screens. An additional stipulation, natural for such kind of experiments, is the constancy of temperature along the whole path of beam propagation. Both are obviously realisable. In comparison with the modified Airy experiment, the method of two-frequency emission/reception has an advantage that the velocity and direction of aethereal wind will be measured immediately in the course of experiment and in calculation formulas (81), not by way of series of measurements, as in the method based on the double quadrant. At the same time, this last method will require much more precise instruments to measure small differences of phases. On the whole, on the basis of considered methods we see that the interferometric method to seek the aethereal wind, whose different versions still were in use, is far from being only either optimal. Much more preferable for this purpose is the modified Airy experiment, which easily can be escaped from masking effects and gives more accurate measurement of calculated parameters. The experiment based on two-frequency emission/reception of EM wave also is more advantageous than interferometric methods, though it requires a precise technique to compare the small difference of phases of received signals. It is advantageous because in this method the masking effects are also absent and consequently, the method is able to answer, just as Airy experiment, the question of aether wind existence and possibility to reliably register it. |
Contents: / 18 / 19 / 20 / 21 / 22 / 23 / 24 / 25 / 26 / 27 / 28 /