SELF |
22 |
S.B. Karavashkin and O.N. Karavashkina |
|
|
|
SELF |
22 |
S.B. Karavashkin and O.N. Karavashkina |
|
|
|
3. Relativistic description of light aberration In the previous item, considering the classical description of aberration effect, we could make sure, this effect arises not because of passing from one reference frame to another, but because to measure the direction to the source, we use a definite directing ruler, whose length is eliminated in the course of derivation. This is why the motion of observer relatively the source and of source relatively the observer give different results. And though at mutual speed small in comparison with the speed of light, the found numerical values are little, the very fact of existence of this difference is important from the view of physics of process.In the analysis of relativistic approach to the aberration problem, this becomes especially important, since “theory of relativity introduces here one basic simplification - it establishes full identity of two cases: moving source of light - stationary observer, and stationary source of light - moving observer” [9, p. 33]. As we could see in previous studies [1], [13] and [14], this simplification is the crux of relativistic method. But the fact that someone voluntarily and without grounds - so to say, by the power of postulates - gave the interrelations between the physical objects convenient for his conception, the nature will not change its essence, but this artificial voluntarism will lead the author to the results that are not associative with the physical phenomenon. And this has a direct concern to the statement of problem of light aberration in the relativistic conception. Basically, having shown the essence of relativistic approach identifying the observer’s motion with the motion of source, and showing these models non-identical, we may stop considering the result of relativistic formalism. With such approach, relativists anyway will not present a complete description of phenomenon, although some particular formulas can be similar in a very narrow range of variation of affecting parameters. The more that at small speeds of mutual motion of objects, in classical formalism also, the cases of moving source and moving observer had approximately same expressions. But this does not mean a least that both models are generally identical. In physics, not mathematics as such, it is important and is not an outward similarity, but the utmost agreement of results with the amount of revealed properties of phenomenon. So in this part of our study we will concentrate our attention not so much on the result as such as on the analysis of logic on whose basis the relativistic formalism has been built. Noting the above, in order to understand correctly the ideology of relativistic derivation of the light aberration law, we have to account that, beginning from Einstein, in the whole literature the aberration problem was derived as a corollary of relativistic summing of velocities. Already at this stage relativists encounter hard difficulties of which indirectly said Born: “We can apply the just used technique: to reveal the affection of Lorentz transformation on the direction of light beam… But this method leads us to some complicated computations, and we would prefer another one; namely, we will apply to the quanta of light the theorem of summing the velocities” [2, p. 294]. Factually, the difficulty is not in the complicated computations. From the view of relativistic approach the matter is too simple. Two equal-rights reference frames are given, of which K is stationary and K' moves relatively K with the speed v. In one of them (any, by the statement of problem) the observer is and in another the source is. The observer has his scale of angular sizes and the source has his; we have to determine the relation of these scales. The record of this statement shows it to be identical, if we consider both from the view of frame transformation and on the basis of speeds summing - in both cases we use the same Lorentz transformation. None the less, this is not fully so. If we consider from the view of metrics transformation, we will follow the way, which Einstein described for some other problems similar to this present. “Consider a body at rest relatively the reference frame S'. Let x1', y1', z1' and x2', y2', z2' are coordinates of two points of the body. At any (selected by us - Authors) moment of time t in the system S the following relation of these coordinates |
 |
(36) |
is true” [15, p. 154- 155]. Taking (36) into account and taking as the body of which Einstein wrote the deflection ruler, we immediately yield the relationship of angles in the moving and stationary reference frames: |
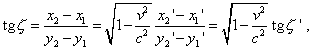 |
(37) |
or |
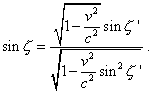 |
(38) |
As we see, the computations are very simple and direct; they are much simpler that those, which relativists suggest with the velocities summing. The only demerit of these computations is - they do not correspond to the regularities of aberration. Actually, if the observer in a moving frame directs the tube of his telescope to the zenith, i.e. |
| (39) |
there will be |
| (40) |
irrespectively of the speed of observer relatively the source; on one hand, it is in full agreement with Airy’s negative result, as relativists estimated it, but on the other hand, it has no relation to the observed facts and result which the classical theory gives, |
| (41) |
Contents: / 18 / 19 / 20 / 21 / 22 / 23 / 24 / 25 / 26 / 27 / 28 /