SELF |
24 |
S.B. Karavashkin and O.N. Karavashkina |
|
|
|
SELF |
24 |
S.B. Karavashkin and O.N. Karavashkina |
|
|
|
Namely this circumstance, which relativists undoubtedly understood, and above corollaries, which relativists have calculated for themselves, caused the creation of the second relativistic interpretation of the ruler measurement. “Let l0 be the ruler length in the reference frame S' in which the ruler is at rest: l0 is called the natural length of ruler (the length at rest). Two ends of the ruler have coordinates, say, x'1 and x'2, so that x'2 - x'1 = l0 . When observing this ruler from the frame S, in accordance with Lorentz transformation we have |
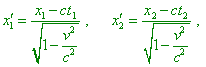 |
(57) |
where x1, t1 and x2, t2 are the coordinates of points x'1 and x'2 in the frame S. Let now we want to measure the ruler length in the frame S; this means that we have to determine the coordinates x1 and x2 simultaneously (? - Authors) relatively the clock of the frame S - we have to assume t1 = t2 . Making so and subtracting the first of equations, which we wrote from that second, we yield |
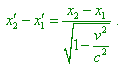 |
(58) |
Assuming x2 - x1 = l , we can write |
| (59) |
This formula corroborates that the ruler length in the frame S appears decreased” [2, p. 241- 242]. So we see from relativists not the efforts to surmount the discrepancies but a simple and quite rough substitution of non-simultaneous measurement of length by that simultaneous. We have multiply encountered such ‘convenient’ substitutions, when analysed different aspects of Relativity in [1], [13], [14]. And this is not ‘an inaccuracy of interpretation’ of a particular author. From the first statement of problem, which forbids to equalise the times of registration of the start and finish of ruler, there follows the basic equation for the speed summing theorem, and from the second formulation there follows the rule to transform the metrics in the relativistic conception. Both approaches are present in all literature on special relativity, beginning with the monographs and papers by Einstein, and both interpretations give different results, which suits to the needed case. The natural question to relativists is, which of statements of problem is correct? If we had no right to register the intervals simultaneously, we have to admit, the change of metric obeys the expression (53), and consequently the transformation of metric does not exist, since we can transmit it in unchanged form from one frame to another. And this concerns both spatial and temporal metrics. In its turn, it follows from this that Einstein - Minkowski 4 D interval is illegal, while it is the basis of transformations that showed the 4 D interval illegal. After the laws of mathematics, this speaks of wrong premise of the relativistic conception. If we consider the possibility of simultaneous measurement of intervals within one frame, we will come to Einstein’s transformations (36), from which in the aberration law there follow absolutely other angles irrelevant both to classical formalism and practical measurement. Moreover, from (59) there follows the conclusion which is fully absurd from the view of physics and the very relativistic conception. To see it, let us draw our attention to, what namely M. Born defined as lengths included into the right and left parts of (59). He thought under l0 the section being at rest in relation to the moving coordinate system, and under l - a related section from the view of stationary coordinate system. It follows from this that at v = c the length of finite section of length in moving reference frame will appear zero from the view of stationary frame, but the section itself will not turn to zero, as relativistic conception interprets it in moving frames. Furthermore, it can have any size, up to the universe, but from the view of stationary frame, its length will anyway remain zero. To develop this aspect of the problem, we can vary the experiment, trying to measure the section of length located in the stationary coordinate system from the view of moving coordinate system. With it, strongly following the second statement of problem after Born, we will yield |
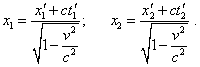 |
(60) |
Further, in full accordance with the principle of equal rights of all reference frames, we can write t'1 = t'2 , from which we yield |
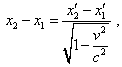 |
(61) |
and finally |
| (62) |
In other words, a section of length in the stationary frame has been reduced to the same measure from the view of observer in the moving frame, so the measures appear mutually identical. The measure in moving frame has reduced relatively the stationary frame, and the measure in stationary frame reduced in the same proportion from the view of moving frame. If now one of observers transmits his measure to another frame and then will measure this measure from his frame, he will register the squared change of length. From this the observer can make two different conclusions. In accordance to this first, he can conclude, like relativists do, the squared change of metric of moving frame. In accordance with the second, he, like practical metrologists do, will conclude of the features of instruments he used. He will repeat his measurements with another technique, or rather with several techniques, will take into account the features of frames and will decide on the basis of combined study. And he will make just the decision of which the opponents say: if the frames were equal-rights and reduction was same, the reduction of space metric is absent, but exist only the features of measurement, which we have to account to keep our experiments metrologically correct. In this case, just as in first case, the 4 D interval fully loses its validity, as with the change of technique of measurement the conditions of transformation which we have to use also change. Thus, we see that in deeper analysis both variants of measurement of the ruler length do not satisfy the postulates of relativistic formalism. So it is quite understandable when relativists feel hurt by their opponents who suggest other measurement techniques, which give other results, different from the relativistic predictions. The difficulty is not in these techniques but in fact that Relativity has been built, or rather tailored, on a very narrow (and far from being objective) underpinning of particular speculative experiments, which fault with a least variation of the statement of problem. In this light, even if in limits of very rough approximations in one of models - namely, in the model of moving observer - relativists would yield a similar approximation, in transition to the model of moving source this approximation already is violated. But if on the basic conclusions we try to complicate the problem, introducing the simultaneous motion of the source and observer, the relativistic conception will give results even farther from the truth. And if we try to consider the case of telescopic systems, in which, as we said, the beam propagates along the broken line, then again Relativity, operating exceptionally with Lorentz transformations, appears unable to provide real results. Namely because it has been built on the simplified underpinning of wrongly interpreted Michelson - Morley experiments. To the point, the conventionally comparable at small speeds approximation of relativistic conception with the classical conclusion in case of moving observer has a cause that Lorentz transformation and Fitzgerald hypothesis have been based on the model of Michelson - Morley experiment, similar to the model on whose basis the aberration effect was calculated in classical formalism. We can easily make sure, looking at Fig. 6.
|
|
Fig. 6. The model to measure the angle of beam aberration with the measurement of ruler located along the axis y' of moving reference frame
|
In this Figure we see the model of aberration of light
emitted by the stationary source. The beam passes through the measurement ruler that has a
strongly vertical position in the moving (dotted) reference frame. But there is also the difference. If we consider Fig. 6 from the view of classical formalism, the cause of angle inclination in the stationary frame is the necessity, the beam to hit both mirrors at the ends of moving measurement ruler. If we consider the same scheme from the view of Fitzgerald hypothesis, the angle inclination will be caused by the space-time transformation in moving frame, due to which in this frame the observation angle is changed by some aberration angle. And this divergence in classical and relativistic phenomenology, just as in case of Doppler effect, is the matter of principle, as this means that if the relativistic conception was correct, the aberration effect has not to be observed in wave processes propagation in media, in which the wave speed is constant relatively the medium, and Einstein - Minkowski 4 D space-time interval does not remain. At the same time, R.W. Pohl visually showed this feature of fronts shift with formation of aberration angle on the model, how water waves pass through the moving inlet in the obstacle (see Fig. 7).
|
|
Fig. 7. The scheme of formation of water waves aberration [4, p. 192]
|
“In Fig. 7a, the water waves with the
plane front fall normally on the inlet B. The inlet selects from them a limited,
approximately parallel beam. And in this case the beam limitation is an essential
circumstance. In Fig. 7b we show the same experiment, but this time the inlet B
moves with the constant speed u with the arrow. Now the main beam appears
refracted. With such refraction, the wave propagation R deflects behind the inlet
by the angle It directly follows from Pohl’s demonstration experiment that aberration is inherent not only in light beams, but in acoustic and hydrodynamic waves, too. With it in these media we already may not speak of reference frames deformation either of wave propagation speed remaining in any inertial frame. At the same time in all mentioned media, the conditions at which aberration takes place will be same, as well as same will be solutions yielded on the basis of modelling equations. Thus, we see, the relativistic conception is revealed wrong not in formulas which, as we said above, only reflect the quality of modelling, but in the very description of aberration phenomenon. Namely so this conception is unable to account the whole versatility of nuances revealed in varying of modelling schemes; instead to analyse the cause of such limitation, it deepens into a wholesale postulating of physical processes. |
Contents: / 18 / 19 / 20 / 21 / 22 / 23 / 24 / 25 / 26 / 27 / 28 /