SELF |
44 |
S.B. Karavashkin and O.N. Karavashkina |
|
|
|
SELF |
44 |
S.B. Karavashkin and O.N. Karavashkina |
|
|
|
True, the experiments ‘without crystals’ have been conducted with electrons also. “The first experiments corroborating the de Broglie hypothesis have been carried out on crystals that are most convenient diffraction lattice created by nature to observe the diffraction of electron waves. Further, a number of diffraction experiments similar to the classical experiments that are well known in optics has been done with electrons. Diffraction of electrons has been observed at the edge of semi-finite plane, on two splits and so on. The experiments have been done on the diffraction of electrons in a heterogeneous electric field that took part of an analogue of Fresnel’s bi-prism. All these experiments corroborated the presence of wave properties in electrons” [3]. In particular, “to reveal, whether the individual particle has wave properties, the team of our physicists led by V.A. Fabricant did in 1949 the diffraction study with a very weak beam of electrons. In these experiments, the time interval between two sequential passes of electrons through the crystal was 30 000 times larger than the time during which one electron passed the whole instrument. Thus, electrons diffracted in the crystal one by one; their interaction with each other as the cause producing the diffraction pattern was fully excluded. The qualitative appearance of distribution of the diffracted electrons in the photographic plate is shown in Fig. 3. When short duration of the experiment, the points on the plate related to the hits of electrons are distributed occasionally (Fig. 3a). But when quite long duration of the experiment, the distribution of points gains the shape of concentric rings (Fig. 3b) typical for diffraction on a poly-crystal. Thus, it was proven that the wave properties are inherent in a single electron” [3]. |
a b |
Fig. 3. Distribution of diffracted electrons in the photographic plate: a – when short-duration experiment, b – in case of long-duration experiment [3]
|
At the same time, “we cannot imagine a particle distributed in space. It hits at some definite place of photographic plate and causes darkening of one grain of photographic emulsion. As the experiment shows, the hit of separate particles to definite places of plate is occasional: sometimes several particles at once can hit almost to same place, sometimes they appear far from each other … Thus, in case of diffraction of particles the degree of darkening of different parts of plate we interrelate with the probability of particles hitting onto these parts of plate. While in case of light … the degree of darkening is in proportion with the squared amplitude of the wave of light” [12, p. 30]. Namely because of this basic distinction between an electron and wave of light, in all cases there was produced an inhomogeneous field that might in some way change the trajectory of electron, while in case of EM waves there is no need in these special conditions and two light beams are able to interfere with each other without additional fields. And in case with diffraction of a very weak beam of electrons, the conclusions of investigators were in a clear disagreement with the results of experiment. Should a single electron, in a full correspondence with the optic analogy, was a wave in space, in short experiments they would see not separate dark points but an analogue of insufficiently developed holography, when in the whole plate they would see fragments of interference pattern from each (!) electron and their assemblage. On the contrary, the experiment corroborates, the electron behaves in the interference experiment as a particle, and the cause of interference is not the wave interior structure of electrons but some non-accounted before properties of interaction of electrons with substance that one did not try to establish, taking as the fact that the wave-particle duality exists, is unavoidable and even comfortable. At the same time, when we identify the interference processes of waves and electrons, deliberately retaining the paradox in the heart of quantum conception, it had to tell on physical models and on the quality of modelling, making it also discrepant. Brillouin wrote of it so: “We will never success to see straight the primordial components of matter but we imagine them trying to guess their behaviour and giving them some strange properties in order to to coordinate most mysterious experiments. What are these primordial components? Are they particles? Are they waves? We cannot give a definite answer here. Our imagination builds a complicated model of seemed contradictions and the science goes on continuously developing” [5, p. 77]. On the other hand, such admission confirms that the scientists are helpless in the situation, as it is clear, the science development, in particular of some theory containing an unsolvable basic, philosophical and gnosiological discrepancy, degenerates into the imaginary development, as the theory based in its evolution on paradoxical postulates produces the same paradoxical corollaries and conclusions that forms false understanding of processes and phenomena. Thereupon the very science stops to serve – to surmount the discrepancies and paradoxes preventing to grasp the true interrelations of natural phenomena. In the quantum-wave theory, the paradoxical corollaries immediately follow from the statement that in the interaction with the substance the electrons behave as de Broglie waves. Actually, according to this hypothesis, “we have to associate the particle with a pulse p and energy E moving with the axis x, using two relationships |
| (1) |
with a wave of infinite extent |
| (2) |
This wave propagates along the axis x with
a definite speed – the phase speed u” [2, p. 109]. Thus, according to de Broglie, a particle has
to gain the properties of monochromatic coherent wave and to lose its finite geometric
size, and not only at the moment when it interacts with the substance but generally. When
the electron flies to the target, it can ‘feel’ this target, only having
approached it immediately; it would be illogic, this electron to have finite size before
interaction with the target, at the moment of interaction to turn into an infinite wave
and after the interaction to become again a particle of quantum size. But if the electron
itself is an infinite wave (or the probability to reveal it at some or other point of
space after Born [2, p. 115] obeys the regularity (2), which is similar), such widespread
measurements as the dilation time of turning on the current, the flight time of electron
in vacuum tubes etc. would lose their logic. The probability to find an electron along
whole measured interval would relate not to the period comparable with the frequency of
X-rays along the whole infinite interval, anyway in limits much larger than the size of
lab instruments, nothing to say of dilation time to pass a limited interval. Just so from
the very beginning of quantum mechanic formation the de Broglie wave was understood as a
chain of waves. In particular, Fermi, when solved the Schroedinger equation for a point on
an infinite line (the model of free electron) and encountered the disappearance of wave
function discreteness, expressed, after other supporters of photon theory, the following
premise: “Let there are
no abrupt discrete energetic levels but instead them are ‘blurred’ levels
corresponding to ‘blurring’ the wave function u (x) across the
interval |
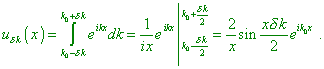 |
(3) |
Such solution already can be normalised
with very small
|
|
Fig. 4. The ‘wave packet’ for the function
u
|
But this is not a real solution of the problem. First, the
function (3) and the de Broglie function (2) are basically different. Second, the wave
chain in (3) has a spectrum, and noting the small size of electron, the spectrum will be
vast and it cannot be limited by a small It was Born who suggested the today conventional interpretation. From the point of this interpretation, the whole course of events in the physical system is determined by the laws of probability. Then to such or other position of a particle in space there will correspond some probability determined by the de Broglie wave associated with the state of particle. Thus, the mechanical process is entailed with the wave process – the process of propagation of probability wave. This last obeys the Schroedinger equation whose importance is to determine the probability of any variant of the course of events in the mechanical process. If, for example, at some point of space the probability wave has zero amplitude, this means that the probability to reveal an electron at this point is infinitesimal” [2, p. 114–115]. |
Contents: / 43 / 44 / 45 / 46 / 47 / 48 / 49 / 50 / 51 / 52 /