V.6 No 1 |
49 |
| On the wave-particle duality | |
|
|
V.6 No 1 |
49 |
| On the wave-particle duality | |
|
|
3. Modelling of dynamic field of an atom In our works we multiply studied different aspects of dynamic field of atom. In [10] we have modelled the dynamic field of nucleus and orbital electron; in [11] – the excitation of orbits by the external electric field. In the present problem we will model the total field of nucleus and exterior electron in surrounding of atom, in supposition that the following modelling of interaction of atom with the flow of electrons will be weak and will insufficiently affect the orbiting of electron, – i.e., with exception of quantum-mechanical limitations and statistical averaging of parameters after de Broglie, we will premise a weak interaction of electrons with the field of atom, the same as Born did. Besides, lest to complicate the solution, we will disregard the dynamic field of nucleus being able to change a little the solution but not the general type of solution. After this simplification, the scheme will take the appearance shown in Fig. 11. |
|
Fig. 11. The calculation scheme of dynamic field in the surrounding of atom
|
In this scheme we show atom as some skeleton with a positive charge +e to which we attributed the origin of coordinates xOy and electron orbiting around this skeleton in the orbit external for the skeleton. The total field we observe at some point P which generally can be placed out of either within the orbit, only not too close to the skeleton, lest to violate the given simplification. In [10] we have gotten over the Bohr’s principle of
electron non-radiating in its orbit. Proceeding from this and from a simple mind that
according to multiple experiments, free electron has an electric field, and ion which we
took as the skeleton has the electric field, too, and in joining these fields, the total
field can in no way ‘switch off’, – at the point P we have to detect
some total field |
| (22) |
As we think the field of skeleton stationary and ignore other electrons which can be in this skeleton, we can approximately think its electric field as Coulomb’s field. This means, according to our scheme, |
| (23) |
The forces out of atom we will think positive and towards the atom – negative. To find the field of electron, we have to account some dilation of the field propagation to the point P that takes place due to the motion of this electron. To account this dilation, let at some moment of time the electron is at the point O' . The distance from it to the observation point P is |
| (24) |
If the field propagated with the speed c, it reaches the observation point through the time interval |
| (25) |
During this time the electron will displace to the position O'' ; at this point |
| (26) |
As the position of electron at the point O''
is simultaneous with the field wave arrival to the point P, we have to
express l in (24) through |
| (27) |
We yielded the transcendent equation to find the distance from electron to the observation point with account of dilation of field propagation. We can approximately solve this expression for thermal orbital electrons in the near of atom for which the condition |
| (28) |
is approximately true. With it |
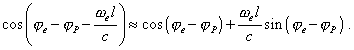 |
(29) |
Substituting (29) into (27), we come to the quadratic equation |
| (30) |
As the distance l can be only positive, this equation has one solution |
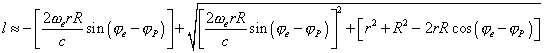 |
(31) |
and we can use it to find the field of delaying potential in the near of atom. With account of (31) we can write |
| (32) |
Contents: / 43 / 44 / 45 / 46 / 47 / 48 / 49 / 50 / 51 / 52 /