SELF |
46 |
S.B. Karavashkin and O.N. Karavashkina |
|
|
|
SELF |
46 |
S.B. Karavashkin and O.N. Karavashkina |
|
|
|
2. Diffraction of electrons on a single atom in the quantum-mechanical description “A simplest problem is to consider the electron scattering by single atoms. A beam of moving electrons is described by a plane monochromatic wave eikz propagating along the axis z with unity amplitude and wave vector k, and the module |
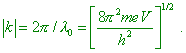 |
(6) |
Atom is considered as a spherically
symmetrical region with the (non-zero) potential Here we have to make a pause in our consideration of conventional approach to resolving this problem, in order to draw attention that the Born approximation is based on the possibility for the potential field of atom to interact with the de Broglie probability wave. Supposedly, electron, neutron or molecule have such property before the interaction with atom. But it means that such probability wave has revealed itself even in absence of any scattering centre. Taking, for example, two beams of monochromatic electrons and directing them onto a screen, we could expect an interference pattern like shown in Fig. 8 for surface waves.
|
|
Fig. 8. Interference of the surface mechanical waves from two pointed sources, http://physics.nad.ru/Physics/Cyrillic/2wa_tmp.htm
|
But in case of electrons such pattern is basically impossible. For it, the distribution of electrons radiated by cathode or electron gun has to have the appearance shown in Fig. 9, which is in full accordance with the Born representation of physical interpretation of the de Broglie wave.
|
|
Fig. 9. Visualisation of the de Broglie wave after Born
|
Actually, as we could make sure in the introduction, Born has introduced namely the statistic substantiation of the de Broglie wave. Again, “if, for example, at some point of space the probability wave has zero amplitude, this will mean, the probability to reveal an electron at this point is infinitesimal” [2, p. 115]. Consequently, the electrons before meeting the barrier have to be already redistributed according to (2), i.e. to produce the longitudinal wave whose length has to be comparable (in case of diffraction on a crystal) with the inter-atomic distance, within the range of X-rays. On the other hand, if in accordance with the quantum-wave
interpretation electrons are not distributed so, Born’s physical substantiation loses
its validity, and we have to think an electron as a wave packet, – which, as we also
saw in the introduction, adherents of quantum conception think unsatisfactory. And not in
vain. Besides the known discrepancies related to blurring of wave packet in time, such
interpretation cannot substantiate the quantum size of electron with little But the main is, even if we do not deepen into the Born’s interpretation of the de Broglie wave, it is basically impossible to yield the diffraction pattern on the atom on some average potential. |
Contents: / 43 / 44 / 45 / 46 / 47 / 48 / 49 / 50 / 51 / 52 /