т.4 No 1

5

О градиенте потенциальной функции

С этой точки зрения можно рассматривать модель поля пульсирующего источника в виде системы эквипотенциальных линий с убыванием амплитуды потенциала с увеличением расстояния от источника, которые распространяются со скоростью c от источника. При этом эквипотенциальная линия, излучённая источником в некоторый момент  t₀, достигнет исследуемой точки P₀, расположенной на расстоянии r от источника за время

(см. рис. 3), а точки P₁, расположенной на расстоянии r от точки P₀ - за время

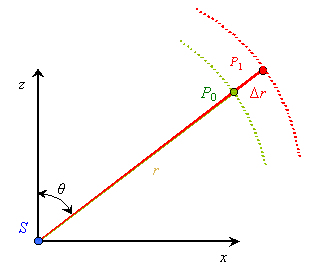Рис. 3. Схема эквипотенциальных линий пульсирующего точечного источника

Поэтому, если мы теперь захотим определить производную от скалярного потенциала по направлению от источника поля, то столкнёмся с тем, что в точках P₀ и P₁, находятся потенциалы, излученные источником с интервалом времени t. В связи с этим, производная по направлению радиус-вектора будет иметь вид

Как видно из (10), динамический градиент (записанный нами с большой буквы для отличия от градиента функции по координатам), состоит из двух слагаемых. Первое слагаемое представляет собой известный нам градиент для стационарных полей, а второе слагаемое учитывает изменение градиента потенциала во времени вследствие динамического характера поля. Но это второе слагаемое и есть временнозависимое слагаемое в выражении (1). Причём следует отметить особенность предельного перехода от приращений функции к производной по времени во втором слагаемом. Несмотря на то, что во втором равенстве вывода (10) мы берём разность потенциалов, излучённых в момент (t -  t)   минус в момент (t), тем не менее, в следующем равенстве знак перед вторым слагаемым не изменяется, хотя t отрицательно. Эта похоже на процесс определения фазы запаздывания сигнала по экрану осциллографа. С одной стороны, при нахождении производной по радиус-вектору мы должны взять в общем случае разницу между дальней и ближней точками поля, но первый из вычитаемых потенциалов излучён источником в более ранний момент, чем второй. Это и приводит к тому, что при вычислении производной знак не изменяется, несмотря на отрицательное приращение времени.