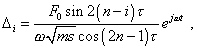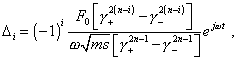т.2 No 1 |
77 |
| Некоторые особенности моделирования вынужденных колебаний | |
|
|
Рассмотренный
матричный метод, как и предыдущий, обладает всеми
вышеописанными недостатками, поскольку
“работает” только при известных значениях |
|
|
(35) |
где а - некоторая
постоянная” [7, с. 296]. С
другой стороны, введение главных координат
равносильно одновременному приведению двух
квадратичных форм T и U к каноническому
виду [7, с. 266]. Из этого можно сделать вывод, что оба
матричных метода способны в аналитическом виде
предсказать только тот факт, что, “если затухание мало, то каждая
амплитуда |
|
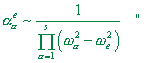 |
(36) |
[7, с. 297]. Точно так же существенными
недостатками обладают и методы решения с
использованием матриц Вороного, Теплица и т.д. В
первую очередь это обусловлено тем, что несмотря
на все попытки упорядочить указанные матрицы и
привести их к диагональному виду, эти методы
хорошо работают, если задана конкретная
последовательность чисел p0
> 0, p1 В противовес этому, точные
аналитические решения, полученные оригинальным
нематричным способом в [1], показывают не один, а
три режима колебаний: периодический ( при |
|
|
(37) |
| при |
|
|
(38) |
| при |
|
|
(39) |
| где |
|
Сравнение (37)- (39) с (36) показывает их четкую детерминированность и по отношению к параметрам внешней силы, и в зависимости от параметров упругой линии, и в зависимости от частоты резонансов. При этом сложность анализа упругой линии не возрастает с ростом n . Эти решения очень просто могут быть продолжены и на линию с распределенными параметрами, что практически неосуществимо в аналитическом виде матричными методами. Внешне может даже появиться сомнение в надежности решений (37)- (39). Тем не менее, во-первых, как показано в [1], все решения (37)- (39) полностью удовлетворяют моделирующей системе дифференциальных уравнений, построенной стандартным образом. Во-вторых, наличие апериодического режима не является столь большой неожиданностью. Косвенные методы, несмотря на ограниченность области применимости и неполноту результатов, в частных случая также подтверждают физическую реальность этого режима колебаний. В качестве примера рассмотрим оригинальный косвенный метод, описанный К. Магнусом [4, с. 282- 285]. Для нас это тем более интересно, что Магнус, представляя указанный метод, также исследует конечную линию с закрепленным правым концом. В связи с этим появляется возможность сравнения результатов. Магнус обратил внимание на
связь между |
|
|
(40) |
При этом он, естественно, нарушил одно из граничных условий, и это должно было привести к определенным проблемам. Обходя их, Магнус предположил, что “при этом в уравнениях движения (8) для отдельных масс ничего не изменится, и мы можем искать периодическое решение, обладающее такой же частотой, что и возмущение, и приходящее либо в фазе с возмущением, либо в противофазе с ним, положив |
|
|
(41) |