СЕЛФ |
6 |
| С.Б. Каравашкин и О.Н. Каравашкина | |
|
|
СЕЛФ |
6 |
| С.Б. Каравашкин и О.Н. Каравашкина | |
|
|
Действительно, опираясь на четыре условия, сформулированные Эйнштейном для гравитирующего поля: " 1. Все компоненты метрики не должны зависеть от времени x4 . 2. Равенства g 3. Решение должно быть симметричным в пространстве вокруг начала координат, т.е. переходить само в себя при ортогональном преобразовании координат x1, x2 , x3 (вращении). 4. На бесконечности
должны обращаться в нуль все величины g |
[21, с. 200], Шварцшильд, недолго думая, вводит метрику следующим образом: "Если время обозначить через t, а прямоугольные координаты - через x, y, z , то очевидно, что наиболее общим линейным элементом, удовлетворяющим требованиям 1- 3, является следующий: |
| (14) |
здесь F, G и H - функции величины r = (x2 + y2 + z2)1/2 " [21, с. 201]. Из (14) мы видим, что Шварцшильд на основе стандартной прямоугольной системы координат ввел некоторую нелинейную метрику, в которой мера длины вдоль каждой из осей изменяется вдоль оси, да к тому же и время в каждой точке этой системы отсчета некоторым образом зависит от радиус-вектора. Возникает простой вопрос: а каковы основания для введения метрики именно в таком виде? Может быть, это обусловлено уравнениями (12)? Нет, до них рассмотрение еще не дошло, с ними Шварцшильд будет оперировать позже. Может быть, это определено условием 3 о сферической симметричности в пространстве? Тоже нет, и следующий шаг решения показывает это. На этом шаге Шварцшильд переходит к сферическим координатам по стандартным формулам ортогонального преобразования |
| (15) |
При этом он приходит к новой, также нелинейной метрике |
| (16) |
"При этом элемент объема в сферических координатах равен |
| (17) |
так что якобиан
преобразования от старых координат к новым,
равен r2sin |
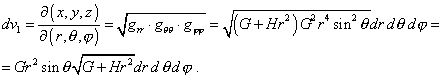 |
(18) |
Так что последующим своим шагом, вводя преобразование |
| (19) |
Шварцшильд уже не мог удовлетворить равенству |
| (20) |
поскольку он должен был удовлетворить иному равенству |
| (21) |
Но если в нарушение условия равенства якобиана единице Шварцшильд даже и пошел на преобразование (19), то тут же снова попал в полосу следующего нарушения математического формализма, которая тянется с самого начала вывода. Ведь при введении новой нелинейной системы отсчета (19), метрика его приняла следующий вид: |
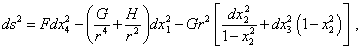 |
(22) |
или с учетом введенных им замен |
| (23) |
Из (23) с учетом записанного им условия для определения |
| (24) |
Шварцшильд приходит к системе равенств, определяющих f1 , f2 , f3 : |
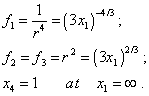 |
(25) |
Но из полученных доопределений (25) можно без нахождения уравнений поля сразу определить два исходных параметра G и H. Действительно, с учетом (22), (23) второе равенство в (25) может быть записано следующим образом: |
| (26) |
откуда |
| (27) |
С учетом (27), а также снова (22), (23), имеем на основе первого равенства (25) |
| (28) |
откуда напрямую следует |
| (29) |
Теперь с учетом (27) и (29) исходная метрика (14) принимает очень простой вид |
| (30) |
который не требует ни дальнейшего нахождения потенциалов поля, ни столь неочевидных преобразований в нелинейных и неинерциальных системах отсчета, ни самих переходов в неинерциальные системы отсчета. Причем полученный результат однозначен и вполне ожидаем, поскольку задан условием для определения определителя, которым оперировал Шварцшильд. Ведь (30) практически идентична метрике Минковского для пустого пространства, отличие только в неопределенном метрическом тензоре |
| (31) |
Содержание: / 1 / 2 / 3 / 4 / 5 / 6 / 7 / 8 / 9 / 10 / 11 / 12 / 13 / 14 / 15 / 16 / 17 /