V.5 No 2 |
29 |
| On basic formalism of special theory of relativity | |
|
|
V.5 No 2 |
29 |
| On basic formalism of special theory of relativity | |
|
|
On basic formalism of special theory of relativity S. B. Karavashkin and O.N. Karavashkina Special Laboratory for Fundamental Elaboration SELF 187 apt., 38 bldg., Prospect Gagarina, Kharkov, 61140, Ukraine phone +38 (057) 7370624; e-mail: selftrans@yandex.ru , selflab@mail.ru http://selftrans.narod.ru/SELFlab/index.html http://selftrans.narod.ru/index.html We will study Lorentz transformation for speeds and accelerations, how do they satisfy the self-consistence of the group of metamorphisms and whether it is legal to join formally the concepts of invariant and 4-D interval. In these frames we will check, whether there are conserved the regularities of accelerated motion in inertial reference frames, the law of vectors addition and reality of relativistic reduction of bodies, and whether it is legal to study the non-uniform motion of bodies with respect to their intrinsic frames. Basing on this analysis, we conclude that the formalism of special theory of relativity is unable to solve the kinematic and dynamic problems of bodies. Keywords: special theory of relativity, speeds summation law, invariance, Minkowski space, groups of automorphism, transitivity axiom, space-time transformation, 4-D acceleration, intrinsic time, intrinsic reference frame Classification by MSC 2000: 83C05, 83C57, 83C75 Classification by PASC 2001: 04.20.Cv, 04.20.Dw, 04.20.Ex, 04.40.Dg, 04.70.-s, 04.70.Bw, 97.60.-s, 97.60.Lf 1. Introduction In the previous works [1], [2], [3], [4], studying the issues related to the conceptions of special and general Relativity, we multiply touched different aspects of relativistic theory and showed the bankruptcy of this theory phenomenologically and mathematically. But every time the basic aspects of the very theory of special relativity (SR) - such as speed and acceleration of body in SR, self-consistence of the group of Lorentz transformation, physical meaning of Minkowski’s 4-D interval etc appeared some aside from the main lane of our study. Now we will fill this gap, devoting this paper specially to the basic aspects of SR and analysing the problems of this conception. 2. Accelerated motion of body with respect to inertial reference frame in relativistic conception To begin, let us consider in frames of SR a problem, trivially simple in classical physics - an uniformly accelerated motion of a body with respect to some inertial reference frame (IRF) which is known to be the basis of both kinematics and dynamics. We will not premise any gravity fields which, as relativists say, warp the space-time metric. We will seek the law of point mass motion under affection of some force, i.e. we will consider a mere mechanical problem that does not exceed the limits of IRFs, and with it will observe the SR postulates. Furthermore, noting that mechanics of SR draws its attention mainly to transitions from one RF to another, we will consider the law of variation of time-constant acceleration of body in a stationary RF, in passing to some RF K' , also inertial, that moves relatively the initial RF K with some speed v in the positive direction of the axis x. Select on the body’s trajectory three points close to each other; in order to simplify, premise the acceleration to be directed also in x. According to Lorentz transformation, these sections of trajectory will be interrelated as |
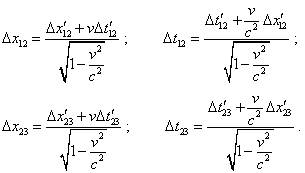 |
(1) |
Thus, the momentary values of speed at the intervals |
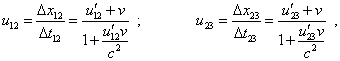 |
(2) |
which is in full accordance with the theorem of relativistic speeds summation. Basically, the expressions (2) are quite trivial and it seems that, going on finding the ratio of increments to the values of related time intervals, we could determine the transformation of body’s acceleration in passing from one RF to another. But there arises the problem that is absent in classical physics. Accordingly to mathematical laws, in finding the second derivatives, one of the main condition is that “the value dx (in this case the increment of argument with respect to which we differentiate - Authors) has one and the same value for all points of the considered vicinity of the point x0” [5, p. 179]. In case of Lorentz transformations this condition is invalid. Actually, substituting (2) to (1) and noting that with uniformly accelerated motion |
| (3) |
we yield with |
| (4) |
the following equality: |
| (5) |
from which it follows that |
| (6) |
So we may not straight determine the relationship in the acceleration value in mutually moving RFs, in frames of relativistic conception we have to undertake another way to find the second derivative in time. Suppose, at the point (x1, t1) of the trajectory in the RF K, the momentary speed of body is u1, and at the near point (x2, t2) it is u2 . By virtue of uniformly accelerated motion, these speeds will be interrelated as |
| (7) |
Then, by the analogy with (1) and (2), |
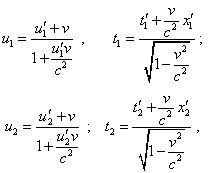 |
(8) |
whence, noting (7), yield |
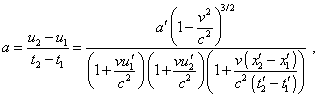 |
(9) |
and tending t2 to t1 and noting that |
| (10) |
we yield in the limit |
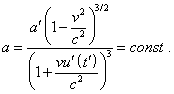 |
(11) |
We see from (11) that in passing from stationary RF to that moving, the constant acceleration becomes time-variable and we can provide its constancy only if |
| (12) |
With it the dotted RF becomes non-inertial and we, on one hand, come to inconsistency with the computations on whose basis we yielded (11), and on the other hand, we automatically exceed the limits of SR validity. Additionally, the dotted frame cannot be the intrinsic frame for the accelerated body, as at zero speed of body in this frame we yield quite strange relation |
| (13) |
This evidences that the IRF equivalence principle is violated in Lorentz transformations based on the inner inconsistency of the very Lorenz transformation, which we will show below. The same as we may not say that to find the body’s acceleration, we have to pass to a non-inertial RF or to account the fictitious gravity field warping the space-time. As we already said, the whole calculation was made in IRFs, in full accordance with the methodology of kinematics, although the relativists, in full discrepancy with the laws of mechanics, determine the acceleration namely introducing the fictitious 4-D vector of acceleration and, additionally, in the intrinsic RF that in case of accelerating body is incompatible with the idea of IRF. To make sure that such definition of acceleration is artificial, let us analyse the substantiation of this definition. |
Contents: / 29 / 30 / 31 / 32 / 33 / 34 / 35 / 36 / 37 / 38 / 39 /