SELF |
38 |
S.B. Karavashkin and O.N. Karavashkina |
|
|
|
SELF |
38 |
S.B. Karavashkin and O.N. Karavashkina |
|
|
|
If we lift the basic mistake, then, noting the above feature, the whole mathematical tool of Minkowski formalism will considerably change. First of all, Lorentz transformation already cannot be represented as rotation in a complex plane. There has to be the sum, not difference of quadrates in the denominator of these transformations. The rotation angle also will stop to be complex. Invariants in this complex space also will be other and, of course, we may not identify them with (96). Proceeding from this, the relationship of time delay and decreasing 4-D interval loses its sense, as (96) is not an interval in a complex space. The fact that this expression decreases with growing speed of the body only adds more paradoxes to this expression, as the decrease of this pseudo-interval is caused not by transition from one RF to another, it occurs in consideration in the same RF. We can easily illustrate it with the help of one of multiple relativistic ‘explanations’ of twin paradox.
|
|
Fig. 1. Illustration of twins C and C’ motion in Minkowski space [12, p. 83, Fig. 16]
|
In the diagram shown in Fig. 1 we see a space-time trajectories of motion of twins C and C' in the plane (x, t) . Proceeding from the fact that the very RF (x, t) is inertial, the trajectory of twin C' appears longer. While proceeding from 4-D interval (96), it appears shorter in the same RF in which the length of trajectory of stationary twin C is determined. Actually, the length of 4-D trajectory of twin C is determined by the expression |
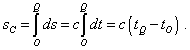 |
(100) |
The trajectory of twin C' moving with respect to the chosen RF consists of five sections three of which are accelerated. Noting that, firstly, from any point of view the accelerated sections can be shortened in time much more than the time of travel and, secondly, we can make them fixed with an arbitrary change of time of travel, expressions like following do not stand any criticism: “After the first accelerated motion, the travellers on ‘Nova’ (the twin C' - Authors) find that they have to fly only a distance |
| (101) |
due to the effect of scale reduction of Fitzgerald - Lorentz” [12, p. 88]. As we already said, the interval of motion can be taken arbitrarily, and the value L (“Before launching, L is just the distance which they have to fly” [12, p. 88]) corresponds to this spatial interval. While the intervals of acceleration are unchanged and do not depend on the trajectory length L, which is well seen in Fig. 1. So we may with enough accuracy neglect the effect of accelerated intervals onto the calculation result, and Born did just so: “ the time spent to the acceleration, turn and deceleration in returning to the point Q can be taken of any smallness in comparison with the time period during which the observer C' moves uniformly in direct and reverse motion, simply making the period of uniform motion quite long [11, p. 249]. So with enough accuracy the length of 4-D trajectory of twin C' is determined in relativistic treatment as |
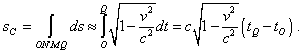 |
(102) |
Comparing (102) with (100), we see that the 4-D interval passed by the moving twin is shorter, though it contradicts even Fig. 1. And noting that the intervals were measured with respect to the common RF, the references to the time reduction are ungrounded. At the same time, the situation with 4-D interval is obviously paradoxical. In this example we see that it is illegal to use Einstein - Minkowski invariant as the interval in complex space. To all these difficulties to represent in the complex plane/space, there is added the difficulty with the time component determining the complex axis of space. This parameter, at least until we prove it experimentally, cannot decrease; this means, in this complex space only increasing trajectories are admissible. These difficulties with Poincare - Minkowski space do not mean that the diagrams in space (x, y, z, t) are admissible under no conditions. In classical kinematics such diagrams are successfully used and do not cause any paradoxes. We only have to operate with symbols and concepts in full accordance with the formalism true for the chosen space. The same in case with Minkowski - Poincare space. In the true metric without Einstein’s invariant taken as an interval, these paradoxes with zero trajectory of the body moving with the speed of light disappear. These limiting trajectories will actually describe a cone, not turn into a point. With it, if the RF is not accompanying, these cones can originate not only from the coordinate origin but also from any given point of space with which we superimpose the light source location. These emitting points can move in space and we can well operate with the multitude of light cones. True, with it we will not see the invariance of interval in the considered RF. But we have not to see this invariance in limits of common RF, since, in accordance with Lorentz transformation, it is revealed exceptionally in transition between the RFs. And the difficulties of completeness of groups of automorphisms of Lorentz transformations, which we studied in the previous items, fully remain and do not depend on the type of space in which these transformations occur. These difficulties, in aggregate with the impossibility to use the Minkowski - Einstein invariant as the interval, make SR an helpless conception. This inability comes to GR through the 4-D interval, whose doubtful invariance is worsened in this case by inconstancy of speed of light; as we showed in the Supplement to [3], it cannot be retouched by the concept of locality. |
Contents: / 29 / 30 / 31 / 32 / 33 / 34 / 35 / 36 / 37 / 38 / 39 /