SELF |
34 |
S.B. Karavashkin and O.N. Karavashkina |
|
|
|
SELF |
34 |
S.B. Karavashkin and O.N. Karavashkina |
|
|
|
From these transitive transformations, one more important conclusion follows. If we suppose the RF K3 moving with the same speed as K2 , but oppositely, i.e. |
| (60) |
then, substituting (60) into (57), we yield |
| (61) |
which fully corresponds to the state of mutual rest of the frames K1 and K3 , and in this way it fully corroborates the equivalence principle for RFs in Lorentz transformations. At the same time, K2 moves with respect to K1 and K3 moves with respect to K2 , and if we follow Einsteinian treatment of real reduction of space-time, the reduction of lengths and time in K3 has to be quadratic in comparison with K1 . On one hand, it is nonsense, but on the other, it leads us up to the essence of problem of reality of reduction in relativistic mechanics. The matter is, when speaking of reality of space-time reduction in moving RFs, relativists rely not on Lorentz transformation in the form (53), which, as we saw above, do not predict a real reduction but only evidence of the feature of measurement of spatial and temporal intervals between the mutually moving RFs. In Einstein’s treatment, the transformations leading to the ‘real’ reduction of space and time have another statement of problem: “Consider a body at rest with respect to the RF S' (to be not confusing further, let us notice, in this case Einstein diverges from his usual designations and denotes with the dot a stationary frame - Authors). Let x'1, y'1, z'1 and x'2, y'2, z'2 are the coordinates of two points of a body. At any moment t, in the frame S between these coordinates the following relationships |
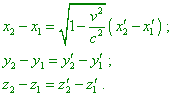 |
(62) |
are true. This shows that the kinematic configuration of a body moving uniformly and directly with respect to some reference frame depends on the speed v of the forward motion. Moreover, the kinematic configuration differs from that geometrical only by the size reduction in relation 1 : (1 - v2 / c2 )1/2 . The relative motion of two frames with the speed v exceeding the speed of light in a void is incompatible with the principles we accepted. It is easy to recognise the hypothesis of Lorentz and Fitzgerald in the yielded equations. This hypothesis seemed us strange, and it was necessary to introduce it, in order to have an opportunity to explain the negative result of Michelson and Morley. Here this hypothesis appears as a natural corollary of accepted principles” [15, p. 154- 155]. None the less, comparing (62) with (53), we see a considerable difference. First of all, it is connected with a temporal parameter which is present in (53) and absent in (62). It is absent namely because the modification of transformation equations was made not by way of ungrounded transformation of the simultaneity concept of which L. Marder said. And, as we showed in our paper [4], it was made in the simplest way: “Let now we want to measure the ruler length in the frame S; this means, we have to determine the coordinates x1 and x2 simultaneously with respect to the clock of the frame S - we have to premise |
| (63) |
[11, p. 242]. But this does not mean that in (62) the time does not transform. Simply in connection with the modification of simultaneity definition, the derivation of time transformation equation has been separated. “The same considerations are applicable to the time interval in two different reference frames S and S' ” [11, p. 242]. ”Consider the clock H' located in the coordinate origin of the frame S' and going p0 times faster than the clock used to determine the physical time in the frames S and S' … As we are determining the time with respect to the frame S, the first of Lorentz transformation formulas |
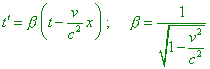 |
(64) |
have to have the following form: |
| (65) |
and as the clock H' all this time remain at the coordinate origin S' , |
| (66) |
which gives |
| (67) |
Thus, if we observe from the frame S, the clock H' will show per unit of time |
| (68) |
periods. In other words, if we observe the clock from the frame with respect to which they move with the speed v, it will appear that they go in 1 : (1 - v2 / c2 )1/2 times slower than the same clock being at rest with respect to this frame” [15, p. 155- 156]. The cited derivation shows that the RF transformation equations were changed by way of direct change of relativity principle. Thereupon, “transformation of Cartesian coordinates of Lorentz - Einstein (62), (68) on which SR is based do not satisfy the relativity principle, despite the common conviction of opposite” [16, p. 4]. And Einstein admitted it: “In accordance with the special theory of relativity, the coordinate systems K and K' in no way are equivalent” [17, p. 618]. In this connection, transformations (62), (68) do not form the group of automorphisms, and we can easily prove it on the basis of complete groups of Lorentz transformation. Actually, if we follow Einstein’s statement, the modified system of equations (62), (68) is equivalent to Lorentz transformation. In this case(62), (68) have to satisfy the property of transitivity, just as Lorentz transformation has to. To check it, suppose that observers are located in the origins of their RFs K1 , K2 , K3 and their clocks are stationary in their RFs. Then |
| (69) |
and |
| (70) |
Hence, |
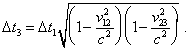 |
(71) |
Now, transforming directly from K1 to K3 , yield |
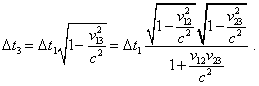 |
(72) |
Comparing (72) with (71), we see the solutions non-equivalent. Consequently, (68) does not satisfy the transitivity condition of the group, in distinct from original Lorentz transformations - this means, they are not a group. Similarly, taking instead clocks some etalons of length, we can find that the spatial transformation of (62) also does not satisfy the property of transitivity and hence also is not the group of automorpisms. In this way we corroborated Denisov’s statement that (62), (68) do not satisfy the principle of RF equivalence, just as they do not satisfy the invariance of 4-D interval. We can easily make it sure, checking additionally, how (62), (68) do satisfy the basic principle of 4-D metric invariance. For it, it is sufficient to pass in these relationships from finite differences to differentials and to substitute the result into the identity |
| (73) |
postulated by Einstein. With it we will yield |
| (74) |
As we can see from (74), the equality of left and right parts has been achieved only in mutually stationary RFs, and this proves our statement. In this way we also prove that the transformation on whose basis relativists conclude the real reduction of space-time continuum, and Denisov, in particular, pointed it: “Thus, as opposite to declarations, SR factually does not satisfy the relativity principle, as it proceeds from relativistic invariance of such or other mathematical equations irrelevant to this physical principle. So transformations (62), (68), being true for a number of mathematical equations, are not true for their solutions, and only these last have real physical meaning. This all has generated a number of ludicrous myths that are just the sacrifices made by physics for the sake of myth of SR beauty” [16, p. 7- 8]. In the view of yielded results, the Readers can better understand the Twin paradox described in [1]. In this paradox, the mutually immovable RFs K1 and K3 , in direct measurement of the time interval, yield the result different from that measured through the moving observer in the frame K2 . Substituting sequentially (60) into (71) and (72), we yield different results. This proves: the cause of twin paradox is just that the transformation system (62), (68) is not a self-consistent group of automorphisms, and therefore it contradicts both the initial postulates and the stipulation of equivalent IRFs, “leading up to degeneration of systematics and, hence, of the structure” [13, p. 349]. |
Contents: / 29 / 30 / 31 / 32 / 33 / 34 / 35 / 36 / 37 / 38 / 39 /