SELF |
30 |
S.B. Karavashkin and O.N. Karavashkina |
|
|
|
SELF |
30 |
S.B. Karavashkin and O.N. Karavashkina |
|
|
|
“The same as in case of speed, in the
theory of relativity instead the three-dimensional vector |
| (14) |
In the special theory of relativity |
| (15) |
so from |
| (16) |
through differentiation we yield |
| (17) |
[6, p. 113], where To understand that the definition (14) is artificial,
follow its derivation which, as we reveal, is grounded on the very general properties of
warped space, although in SR, with its Euclidean spatial metric, this obviously is
excessive and only corroborates that relativists know the discrepancy in this aspect of
their theory. None the less, it is easy to check that relativists introduce the
acceleration in frames of invariant differential operations as follows: “Let at each point of the curve xk = xk (t) there is given a vector with the
components ai (it still is not the
vector of acceleration - Authors). Choose arbitrarily a permanent
point on the curve P and graph the second assemblage of vectors |
| (18) |
Then with the help of relation |
| (19) |
we can invariantly determine the new vector, as in the numerator we see the difference of two vectors at one point. From |
| (20) |
(page 63 of the cited work - Authors) and |
| (21) |
(page 65 of the cited work - Authors) it follows that |
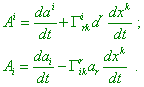 |
(22) |
If we substitute instead t the length of arc s and instead ai - the tangential vector ui = dxi / ds , we will yield in this way the vector of ‘acceleration’ whose components Bi coincide with the left part (of the equation of geodesic line - Authors): |
| (23) |
[6, p. 89- 90]. We can see from this derivation that (14), just as (23),
does not account the above features differentiation within Minkowski 4-D metric caused by
the features of Lorentz transformation. All derivatives, second-order in that number, are
determined, proceeding from the mind that the operation is true, though it has to be
strongly proven. And we see in the derivation the ungrounded transitions from the time
coordinate to that spatial changing not only the meaning of transformations but also the
dimension of the result. But with it, just the prototype of (23) Pauli took as the basis
when finding the concept of acceleration, and not in vain he selected this word by
quotation marks. The vector |
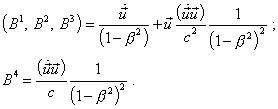 |
(24) |
It follows from (24) that in case of considered problem of direct accelerated motion of the body with respect to the stationary RF |
| (25) |
Thus, |
| (26) |
which means that in relativistic conception, the acceleration time-constant as to IRFs is basically impossible. Moreover, as with the accelerated motion ux grows with time, Bx also grows with time without additional affection, except of force which has to provide the constant acceleration by the statement of problem. This definition of acceleration is not some particular representation of Pauli. Levich defines, similarly, “the four-dimensional acceleration wa as |
| (27) |
[7, p. 219], where t0 is the intrinsic time. Thereupon he comes to the same expressions (24) that define the 4 D ‘acceleration’. |
Contents: / 29 / 30 / 31 / 32 / 33 / 34 / 35 / 36 / 37 / 38 / 39 /