V.5 No 2 |
31 |
| On basic formalism of special theory of relativity | |
|
|
V.5 No 2 |
31 |
| On basic formalism of special theory of relativity | |
|
|
To understand the inner contradiction of such approach to the acceleration definition, we have to clear two basic aspects. First, we have to ascertain the concept of intrinsic time and intrinsic system of coordinates, and on this grounds, second, we have to determine the legacy of finding the derivation in this intrinsic time in case of accelerated motion in relation to the IRF. Accordingly to the most general definition, the intrinsic RF is “an inertial reference frame K* chosen at the given moment of time at the given point M of the medium so that the speed of the point M in relation to K* was zero at the given moment of time; the speed of neighbouring points and of M at other moments of time in this frame can differ from zero. We deal with the use of intrinsic reference frame and intrinsic time in our sensations. Intrinsic time is the invariant characteristic of ordering and every possible inner processes and inner interactions” [8, p. 323]. With it, “it is obvious that the intrinsic systems of coordinates generally do not coincide with the accompanying coordinate system in which the speeds of all particles are always zero; the intrinsic system is inertial, and the accompanying system, of course, generally is not inertial” [8, p. 324]. It follows from this definition that in case of accelerated motion of the body in relation to the IRF, the intrinsic frame is different at each moment of time, and although each of such multitude of frames is inertial itself, we have no right in such multitude of non-identical frames to apply Lorentz transformation even for speeds, as in defining the speed, we have to know two neighbouring locations of points on the trajectory to which there correspond their intrinsic RFs moving with different speeds in relation to the stationary RF. Neglecting these outwardly small values in frame-to-frame transition, we factually distort the result. It is easy to show it even by the example of uniformly accelerated motion. Let at the moment t1 the speed of point in relation to the stationary RF was v1 , and at the moment t2 = t1 + dt its speed was v2 = v1 + dv . It appears that to find the momentary speed through the intrinsic frames, we have now not two but three frames, and two of them move with respect to that third with different speeds. And we have first to convert the speeds into the common RF, and only after it we may calculate. Or we will have to use the stipulation that at the next moment of time the body can shift from the coordinate origin of the intrinsic RF and to take the motion of this body as the motion in relation to two RFs. In this last case, in accordance with the theorem of relativistic speeds summation, we will have at the moment t1 |
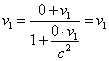 |
(28) |
and at the moment t2 |
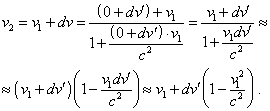 |
(29) |
From (28) and (29) we yield |
| (30) |
To determine the time increment in the conventionally intrinsic RF, we have to apply Lorentz transformation between the coordinates of stationary and intrinsic RF. With it for the moment t1 we yield |
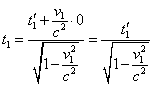 |
(31) |
and for t2 |
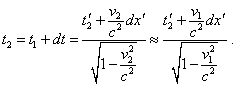 |
(32) |
Consequently, |
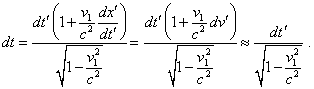 |
(33) |
Basing on (30) and (34), yield |
| (34) |
As we see, (34) is equal neither to (26) nor to the definition (24). Naturally, in case of more general motion (34) will be complicated, but none the less, it also will not satisfy the above yielded expressions. Furthermore, it follows from (34) that, again, with the constant acceleration of a body in the stationary RF, in the intrinsic RF the acceleration will not remain constant, it will increase (not decrease) with the growth of body’s speed. This evidences, firstly, that the differentiation in the intrinsic time is not so simple operation as relativists think. It is insufficient here to put the vectors into coincidence, we have to combine the transformation of RFs, and this, generally, much complicates the differentiation and makes it dependent on the pattern of acceleration and on the trajectory of accelerated body. Secondly, if we pass to the intrinsic RF, it does not lift the contradictions connected with the features of secondary differentiation over time of which we said in the beginning of this item. It was Levich who well understood some of these difficulties: “the formula |
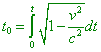 |
(35) |
is often applied to the accelerated
motion, thinking v to be the function of time. However, we have to
note that in special theory of relativity we may not consider the accelerated motion of
reference frames. So the value t0
determined by (35) in case of accelerated motion has not the meaning of intrinsic
time but is a convenient value invariant relatively Lorentz transformation” [7, p. 211]. On the other hand, it did not prevent Levich
from introducing the acceleration in the form (27) as the derivation namely over the
intrinsic time. The same, to avoid this contradiction, Pauli changed the interpretation of
intrinsic time: “so in
this case it would be convenient instead the arc s to introduce the intrinsic
time |
| (36) |
It determines the time registered by the clock moving in this world line. So for the coordinate system in which the clock is currently at rest |
| (37) |
[6, p. 98]. From Pauli’s definition we first of all see that he joins the ideas of intrinsic and accompanying RFs. The intrinsic frame can move with the body along the trajectory exceptionally in case of uniform direct motion of the body in relation to the IRF. Generally, the clock will not move along the world line. At each new moment of time there will arise a new intrinsic RF with new parameters and other Lorentz transformation with respect to the stationary RF. Secondly, in general case, in this intrinsic RF, in relation to the clock being at rest at its coordinate origin at the initial moment of time, at the next moment |
| (38) |
as the body already is not at the coordinate origin. Hence, we actually do not yield the simplification because of which the relativists introduce the intrinsic RF. On the contrary, the necessity to account the additional transitions connected with the newly formed intrinsic RFs, in rigorous approach to the mathematical operations, will even more complicate the calculations. The main is that with all these contrivances, relativists did not provide such generality of relativistic kinematics which is necessary to compete with that of classical kinematics. Well, after the authors’ opinion, “this theory (SR - Authors) requires, the mathematical expression of the natural law, which was true at arbitrary speeds, did not change its form in transition, with the help of transformation equations, to new space-time coordinates in formulas expressing this law” [9, p. 185]. As opposite to this, as we clearly saw in the present part of work, the constant acceleration in relation to the stationary IRF retains its constancy in accordance neither with our calculation nor with that relativistic. In all cases it depends on the momentary speed of body at each moment of time, which puts in doubt the validity of the introduced system of transformation based on the constant speed of light and Lorentz transformation. |
Contents: / 29 / 30 / 31 / 32 / 33 / 34 / 35 / 36 / 37 / 38 / 39 /