V.5 No 2 |
35 |
| On basic formalism of special theory of relativity | |
|
|
V.5 No 2 |
35 |
| On basic formalism of special theory of relativity | |
|
|
5. Violated self-consistence of the group of automorphisms for the secondary Lorentz transformations Considering in the previous item the self-consistence of group of automorphisms for Lorentz transformations, we marked that Lorentz transformations satisfy the conditions of group only for coordinate transformations but do not for secondary transformations made on their basis for speeds and accelerations, as well as for the parallel system of transformations introduced by Einstein for the time coordinate as an equivalent to Lorentz transformations. Given the self-consistence of secondary transformations determines the ability of relativistic theory to solve the kinematic and dynamic problems of the systems, we in this item will specially touch this issue and generalise the results of item 2. Let we have two IRFs K and K' and K'
moves in relation to K with the speed v, and let some point material
body moves in relation to the stationary frame with the speed In accordance with laws of kinematics in IRFs, we may show
the vector of speed |
| (75) |
and one of them generally can have an arbitrary direction in space. In the moving RF K' , some vectorial relationship |
| (76) |
will correspond to the resolution (75). Supposing that the vectors To apply this technique, let us determine the relation in |
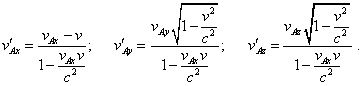 |
(77) |
Similarly, for |
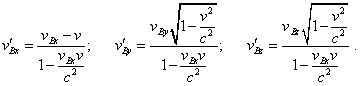 |
(78) |
Thus, basing on (76), |
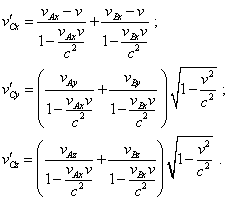 |
(79) |
Then, implementing the direct transformation of |
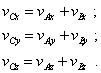 |
(80) |
Consequently, in the direct transformation of vectors yield |
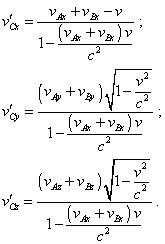 |
(81) |
Comparing (79) with (81), we see, in general case no one projection coincides. This evidences the violated law of vectorial summation in Lorentz transformations. It is significant that we proved with the account of theorem of relativistic summation of speeds with whose help in the previous item we proved that Lorentz transformation satisfies the condition of group transitivity. This means, the theorem itself is true in relativistic transformations, but Lorentz transformations remain their self-consistence of group of automorphisms only for coordinate transformations and are violated in secondary transformations. And Einstein knew of it from the very beginning. Already in his first paper stating the initials of SR he wrote: “the law of parallelogram of speeds in our theory is true only in the first approximation” [18, p. 20]. But the first approximation can relate only to non-relativistic speeds of bodies, where from it straight follows that SR is inapplicable to the studies of objects’ motions with the nearly-light speed, i.e. in the range of speeds to which relativists just relate SR’s solutions. While in the large-speed range, SR remains its conventional validity only in coordinate transformation, which makes it helpless in solving the problems of kinematics and mechanics of material bodies. In distinct from this, the amount of problems solved in Newtonian mechanics is well more versatile. The advantage of Newton’s mechanics is just that the limits of three self-consistent laws are able to cover all the versatility of dynamical problems with small speeds (as to that of light). With relativistic speeds Newton’s dynamics will not lose its advantage, as well as the group of automorphisms of Galilean transformations will remain. Although the changes in modelling of process undoubtedly will take place, - and this is natural, - but these features will account particular deformations of particular bodies and fields, not space-time metrics on the whole, because some body in this space moves with the nearly-light speed. It is basically impossible to substitute these features by the constant speed of light. So all claims that these are relativists who have developed Newton’s dynamics are groundless. This was an imaginary development, as it was made exceptionally by substitution of physical reality by a virtual symbolic representation and worsened by an additional destruction even of the structure of group that follows from the original Lorentz transformations. |
Contents: / 29 / 30 / 31 / 32 / 33 / 34 / 35 / 36 / 37 / 38 / 39 /