V.6 No 1 |
7 |
| On excited state of orbital electron | |
|
|
V.6 No 1 |
7 |
| On excited state of orbital electron | |
|
|
2. Change of Kepler’s law when electron’s orbital motion in the external field To enter the meaning of the issue, consider, how Keplerian law of areas changes for the hydrogen atom interacting with the electric field of general type, and whether this law changes in such interaction. We yet will not account the orbital motion of the atomic nucleus, we will confine ourselves to a simple model of electron orbiting around the nucleus at rest, as shown in Fig. 6.
|
|
Fig. 6. A simplified kinematic scheme of a hydrogen atom in the external time-variable electric field
|
The modelling system of differential equations describing the electron’s motion in this model is |
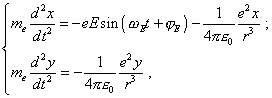 |
(35) |
where e is the electron’s charge, On one hand, the system (35) relates to the trivial modelling of processes in Bohr’s theory. Really, the trivial modelling system of equations is |
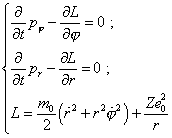 |
(36) |
[7, p. 20- 21]. We see that (35) and (36) differ only by the chosen reference frame - (35) is in Descartes and (36) in the polar system. On the other hand, in (35), except the central field, the external force is also involved, and this distinction matters, as it immediately in the modelling equation accounts the excitation, while the conventional modelling (36) operated only with the stationary frame and estimated the excitation by the level of orbital electron energy change between the stationary states; as we will see below, this is not sufficient. In absence of external field, both frames are identical and describe generally the elliptic trajectory of electron’s motion. In presence of external field, we in general case may not fully identify (35) with linear oscillator, and we can show it mathematically. To do so, multiply the first equation of (35) into y and the second into x, and subtract this first from the second; we will yield |
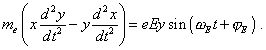 |
(37) |
Given |
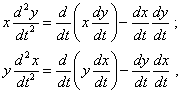 |
(38) |
the left part of (37) will take the following form: |
| (39) |
With it we can write (37) as follows: |
| (40) |
To go on transforming (40), we have to pass to the polar coordinate system, as it trivially follows: |
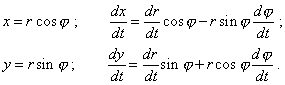 |
(41) |
Substituting (41) into (40), yield |
| (42) |
We see in the left part of (42) the derivative in time of the sectorial speed of electron. Actually, it is known that the sectorial speed of the orbiting body is determined by the vectorial product |
| (43) |
where In its turn, in the plane case, general speed of the body in polar coordinates is |
| (44) |
Substituting (44) into (43), yield |
| (45) |
and this proves our statement. Thus, given (43) and (44), (42) takes the sought form |
| (46) |
In the absence of external field, i.e. when |
it follows from (46) that |
| (47) |
which is the mathematical record of the second Kepler law
that says, in orbital motion the sectorial speed of the body is constant. While in
presence of the external field, it follows from (46) that the second Kepler law is
transformed, due to which the sectorial speed gains periodicity. When the body moved with
the force (the radial angle Now if we premise that in approximation of small amplitude
of the external field the momentary phase |
| (48) |
then in the right part of (46) we have the superposition of two oscillations, |
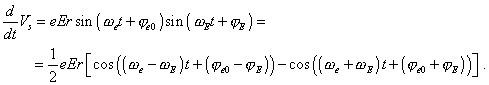 |
(49) |
It immediately follows from (49) that maximal
transformations of electron’s trajectory will relate to the proportional frequencies
of the external field and electron’s orbiting. Namely so, as we cited above, Bohr in
description of excitation wrote: “Now suppose that the electron emits the monochromatic radiation with
the frequency |
Contents: / 1 / 2 / 3 / 4 / 5 / 6 / 7 / 8 / 9 / 10 / 11 / 12 / 13 / 14 / 15 /