SELF |
8 |
S.B. Karavashkin and O.N. Karavashkina |
|
|
|
SELF |
8 |
S.B. Karavashkin and O.N. Karavashkina |
|
|
|
3. Stability of the electron’s orbiting at small external affection The next important issue in constructing our model is to determine the stability of orbiting at small external affection. To clear this issue, suppose that in the stable state the electron moves in the circular orbit. The radius of this orbit R0 is determined by the balance of charge-to-charge attraction and centrifugal force, or mathematically |
| (50) |
where q and me are the charge and mass of electron and v is the orbital speed of electron. Let now, because of external affection, the radius of
electron’s orbit changed by some small value |
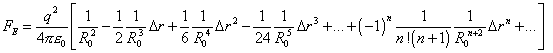 |
(51) |
and |
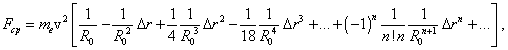 |
(52) |
where n = 0, 1, 2, ... . If now we, in accordance with the sign of radius variation, take as positive the direction of force from the centre of dynamic force outwards, then given (51) and (52), we can write the expression for the resultant that appears in the system because of its excitation: |
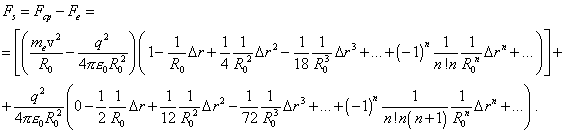 |
(53) |
Noting that the first multiplier in the square brackets turns to zero in accordance with (50), yield |
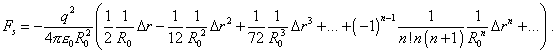 |
(54) |
As we see from (54), the returning force is directed against the direction of orbital radius variation. This evidences that the orbital motion is stable. Furthermore, we see that the series (54) is fast-decreasing; in case of small excitation this allows to linearise the problem, taking as a returning force the expression |
| (55) |
where ss determines the elasticity of constraint. Basing on this derivation, we can prove that the radial excitation of the orbital electron is unable to break the connection between the nucleus and this electron. For it, noting fast convergence of the series (54), it is sufficient to analyse the condition of the sign inversion of the returning force for the first three terms of this series. Taking |
| (56) |
yield |
| (57) |
The sign inversion (57) can take place at |
| (58) |
but the expression in the left part of (58) has only complex roots: |
| (59) |
Thus, with merely radial excitation of electron, this excitation is unable to break the electron’s connection with the nucleus. Consequently, it is possible to break the connection only in simultaneous change of radius and orbital speed of electron, - and we have to account it in modelling of excitation processes. |
Contents: / 1 / 2 / 3 / 4 / 5 / 6 / 7 / 8 / 9 / 10 / 11 / 12 / 13 / 14 / 15 /