V.6 No 1 |
9 |
| On excited state of orbital electron | |
|
|
V.6 No 1 |
9 |
| On excited state of orbital electron | |
|
|
4. The features of the problem of orbital electron’s excitation by the external field Basing on the proven possibility to linearise the problem
for small excitations of orbital electron, we will continue to study our model in which
the electron in the non-excited state moves in the circular orbit around the stationary
nucleus. Besides, to simplify the problem, premise that the wavelength of excitation field
is well more than the area of electron’s orbit. On one hand, this allows us to
premise the field homogeneity at any moment of time in all the studied area, and on the
other it is real, as the typical radiation wavelength for, e.g., hydrogen atom in the
visible part of spectrum is (4101,7 – 6562,85) This model is shown in Fig. 7.
|
|
Fig. 7. General model to calculate the electron’s interaction with the external dynamic transverse electric field
|
Basically, this model is quite trivial and fully corresponds to that which Bohr used and for which neither he nor the following researchers could not find direct full solutions. As is known, namely this caused the quantum-mechanical methods. To try to yield direct full solutions for the linear case, let us some transform the initial model, passing to the reference frame of the nucleus whose axis x rotates with the frequency of electron’s stationary rotation in its main orbit. Noting the possibility to substitute the electromagnetic interaction by a mechanical linear constraint, we come to the model of linear vibrator that vibrates under the rotating external field; its appearance is shown in Fig. 8.
|
|
Fig. 8. The transformed model to calculate the electron’s interaction with the external dynamic transverse electric field in the atom’s reference frame at the external field frequency equal to the double frequency of non-excited rotation of electron in the main orbit
|
In this model, if we write the law of external field variation in its most general complex form |
| (60) |
in passing to Fig. 8 this regularity will take the following appearance: |
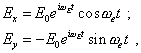 |
(61) |
where From this construction we see that the linearised model has been reduced to the simultaneous affection of transverse and longitudinal forces, which means the system of two equations. Furthermore, to provide the correct transition from the model shown in Fig. 7 to that in Fig. 8, we have to account the feature of passing from the inertial reference frame to that non-inertial. In this connection, there in the modelling equation will appear additional terms describing the mutual affection of transverse and longitudinal force on the pattern of oscillation process. To describe the affection of longitudinal (in Fig. 8) shift of the electron onto the pattern of oscillation process in the transverse direction, we have to account, this longitudinal shift corresponds to the radial shift in Fig. 7. Due to this shift, the Coriolis force deviating the electron transversely arises. The value of Coriolis acceleration is known to be [15, p. 221] |
| (62) |
where |
| (63) |
where The same, to account the affection of the electron’s transverse shift in Fig. 8 onto the pattern of longitudinal oscillations, we have to account that in Fig. 7 this shift relates to the change of the electron’s orbital speed. This change will cause the change of value of centrifugal force, in addition to that calculated in the previous item. We can calculate this addition for the linear approximation as follows: |
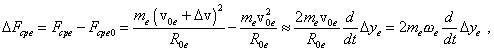 |
(64) |
where Noting these nuances, we may pass to the linear model of our problem. |
Contents: / 1 / 2 / 3 / 4 / 5 / 6 / 7 / 8 / 9 / 10 / 11 / 12 / 13 / 14 / 15 /