SELF |
34 |
S.B. Karavashkin and O.N. Karavashkina |
|
|
|
SELF |
34 |
S.B. Karavashkin and O.N. Karavashkina |
|
|
|
To check the correspondence of the statement of problem to the result of relativistic derivation of Lorentz transformation, suppose, we have two inertial reference frames mutually moving with the speed v. Each of them contains a stationary rod whose lengths are equal from the view of arbitrarily chosen stationary frame, see Fig. 1. |
Fig. 1. Two mutually moving inertial frames with the stationary rods of equal length from the view of stationary (undotted) frame
|
In this problem we can, first of all, according to the relativistic statement of problem, introduce in each frame its own physical time that is detected by synch mutually resting clocks at all important points of this experimental scheme. On this basis we can put in the stationary frame an additional observer at the point x0 . When the end A' of a moving rod crossed this point at some instant t0 , this will detect the start of time intervals in the calculated scheme. We should emphasise, as opposite to relativistic conviction, that the information about the event has to be immediately passed from all clocks of the scheme to some common point, to a common observer; in real experiments no one puts such special stipulation. During some pre-experimental period we can calculate the schemes and provide the experiment metrologically. Then we will do just the experiment, and after it we will work with the yielded results. From the view of this conventional practice it is sufficient, all clocks to be synch in the stationary frame. It will permit us after the experiment, basing on the yielded data, to quite trustworthy determine simultaneous events, equal times and spatial intervals, to match the events and to calculate the paths of all observers and rods. Now let us suppose that the start point of each rod is located at the origin point of its frame. Basing on this conventional practice of experimenting and on our initial data for the stationary frame, let us plot the Minkowski diagrams for the stationary and moving frames, proceeding from the premise that the Einstein – Lorentz transformation is true. For the stationary frame the equations that determine the 4-D trajectory of the rod ends will be |
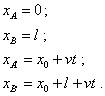 |
(5) |
The Minkowski dynamic diagram plotted on the modelling equations (5) is shown in Fig. 2.
|
Fig. 2. The Minkowski dynamic diagram for the stationary frame. The diagram parameters: l = 1010 m ; v = 0,8 c ; x0 = -1,5 l
|
As we see, the dynamics of rods motion from the view of stationary frame is in full agreement with the statement of problem in accordance with which we introduced in this frame the physical time, so the rods are moving in a plane-parallel manner to the axis x. With it, the related ends of rods meet at the same time, though these events are distanced by the rod length. This is in a full agreement with the above statement that if we introduced the physical time in the frame, this is sufficient, the concept of simultaneity of events distanced from each other to be true in this frame. We can easily check it experimentally if putting additional observers with synch clocks to the points of events. Or rather, in this specific case the observers at the ends of rod AB will detect the simultaneity. Thus, we made sure that at least in the stationary frame the concept of simultaneity of events remote from each other did not loss its sense. |
Contents: / 28 / 29 / 30 / 31 / 32 / 33 / 34 / 35 / 36 / 37 / 38 / 39 / 40 / 41 / 42 /