V.6 No 1 |
37 |
| On correctness of basic postulates of SR | |
|
|
V.6 No 1 |
37 |
| On correctness of basic postulates of SR | |
|
|
Noting the said, to plot the Minkowski diagram for the moving frame, we have to use the modelling system for the stationary frame (5) and conventional Lorentz – Einstein transformation |
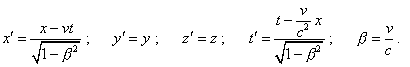 |
(14) |
Substituting sequentially (5) into (14), yield for the ends of rod AB |
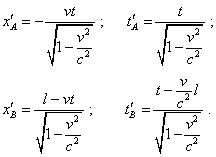 |
(15) |
Similarly for the rod A'B' : |
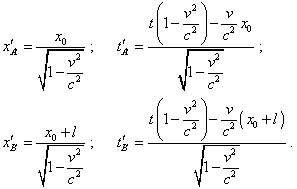 |
(16) |
The dynamic diagram plotted on modelling equations (15)–(16) is shown in Fig. 4.
|
Fig. 4. Dynamic Minkowski diagram for the moving reference frame. The parameters of diagram: l = 1010 m ; v = 0,8 c ; x0 = -1,5 l
|
First of all, as we see from the construction, this diagram is not a result of turn of the diagram built for a stationary frame, it is formed by way of two oblique shear transformations in the axes x and y relatively, as is shown in Fig. 5.
|
Fig. 5. The scheme showing the pattern of geometric transformation of the coordinate system made by the Lorentz transformation
|
We see from this construction that the Lorentz transformation is clearly non-orthogonal and has nothing in common with the turn of coordinate systems around the coordinate origin. Namely so there appeared a complex angle of turn and the transformation coefficients did not coincide. This points, all used today relativistic calculations made with the turn of coordinate system by a complex angle are incorrect. Now let us return to the Minkowski diagram. The line drawn through the limit points of trajectories of both rods in time remains parallel to the initial location of rods; this line is shifted strongly vertically. So we have a strange pattern: on one hand, according to the statement of problem, when Einstein derived his transformation, he introduced the physical time in both frames, while the yielded transformation cancels the physical time in the moving frame. And if we exchange the places of frames, the transformation will cancel the physical time in the undotted frame, where it was also given by the statement of problem. Further, the inclination of line joining the ends of trajectories remains its inclination. This means that all parts of the frame have same pace of time. In this situation the imaginary non-simultaneity which Lorentz transformation introduces is not non-simultaneity. This is easy to show, noting that in the dynamic diagram the ends of all trajectories belong to the line parallel to the initial location of the studied model. Actually, proceeding from this, we can state that non-simultaneity arises not with the motion of scheme elements but it is determined by the initial location of the scheme elements. Write the modelling equations (15) and (16) for the initial moment t = 0 . We will yield for the rod AB |
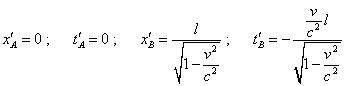 |
(17) |
and for the rod A'B' |
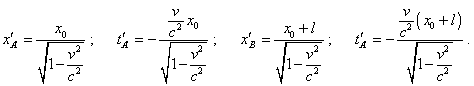 |
(18) |
We see from (18) that the initial spatial and temporal coordinates that determine the value of relativistic non-simultaneity of events depend not only on the rod length and speed of the frame but also on the coordinate x0 of the stationary frame whose absolute value is determined not only by the initial mutual location of the scheme elements but also by the choice of the coordinate origin. At the same time we see from (17) that the initial coordinates of the ends of rod AB do not depend on the parameters of chosen origin of the stationary frame. It appears that dependently on the choice of the coordinate origin and on the pattern of body’s motion, we can really change the absolute value of non-simultaneity of events. This is irrelevant to the claimed one-valued transformation of time by the Lorentz transformation and evidences, the yielded non-simultaneity is imaginary, it is caused by incorrect relativistic transformation. The inclination is now unimportant, as with the arbitrary choice of coordinate origin of the stationary frame and with the infinite number of identical mutually resting inertial frames, the absolute values of non-simultaneity become indefinite. |
Contents: / 28 / 29 / 30 / 31 / 32 / 33 / 34 / 35 / 36 / 37 / 38 / 39 / 40 / 41 / 42 /