V.6 No 1

35

On correctness of basic postulates of SR

Now let us plot the Minkowski diagram for the moving frame. Only note before, according to the conventional relativistic view, we have to yield the graph that will be turned with respect to that in the stationary frame by some complex angle. Such opinion has been rooted from the times of Poincare who in his work “On the dynamics of electron” said the following: “It is easy to see, the Lorentz transformation is nothing else as the turn in this space around the coordinate origin that is considered stationary” [28, p. 478]. Namely proceeding from this analogy, Poincare has concluded that in this space “the invariants different from each other will be only six distances between three points P, P' and P'' and the coordinate origin or, if you wish, two expressions

or four expressions of the same form yielded resulting from any rearrangement of three points P, P' and P''” [28, p. 478]. In this way Poincare factually has anticipated the 4-D interval that directly interrelated the L-postulate and transformation of Lorentz – Einstein. Emphasising this issue, “it would be not excessive to underline the conventional type of graphic image of Lorentz transformation. The turn angle in Fig. 3 is imaginary. Of course, we cannot depict the turn by an imaginary angle.

  Fig. 3. The Lorentz transformation shown graphically

The merits and demerits of graphical depiction of Lorentz transformation are well seen from the following consideration. Let the clock is at rest in the frame K' at some point x'. This physical event at the instant '₁ will be plotted by the first point, at the instant '₂ – by the second point on the axis '. The time interval ' is equal to the length of section from the point 1 to the point 2. In passing to the frame K (turn by the angle ) the section ' turns into the section on the axis . We clearly see, it is senseless to speak, which frame is more correct and which of time intervals, either ', is a true time interval between two events. The defect of geometric consideration is that the interrelation between and ' in the drawing is opposite to that real: in the drawing is less than ', while factually it is more in relation

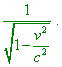The distortion arises because we cannot show in the graph the imaginary value of the angle and substitute it by the real angle” [29, p. 216–217]. Of course, such substantiation of wrong analogy of Lorentz transformation with the rotation by an imaginary angle is incorrect. If the analogy was complete, there can be no miscorrespondence. If the analogy was false, such graphic interpretation is incorrect. So plotting the Minkowski diagram, we will pay more attention to this aspect.

  The second important aspect to which we have to pay attention is the relativity of simultaneity which relativists state. Above we showed, in limits of one frame the simultaneity of events distanced in space remains if in this frame we introduced the physical time. But this does not mean that, as relativists say, the simultaneity of events remains in passing from one inertial frame to another. Rather, if speaking from the point of classical physics, there is no problem in this case, as in this formalism the time is not transformed. But when in relativistic conception the time was transformed, it makes the issue more intricate.

When Einstein derived his transformation, he had to put in agreement the origin of time frames in two reference systems: “let us choose as the zero point of time in both frames the instant when the coordinate origins coincide; then the sought linear equations of transformation will be homogeneous” [27, p. 71]. Factually, the possibility of such operation with the possibility to introduce the physical time in each frame implies the possibility to synchronise two events in one coordinate system in passing from one frame to another. Actually, suppose, we synchronise not through a single event occurring at one point but through two events occurring at two points of the stationary frame. The simultaneity of these two events is fully substantiated by the presence of physical time in the considered frame. These events will give two marks of the time zero point in the moving frame independently of the absolute time which (perhaps) the clocks show at these points of another frame. Thus, two events will factually interrelate the starts of time intervals of two points of both frames. And as the time intervals for the clocks in the moving frame are equal for all its clocks, the following events also will be synchronised in time with each other and with the stationary frame, at least in the beginning of time interval. Noting also that we can manage any number of such synchronised pulses from the stationary frame to the moving frame, all clocks in the moving frame in transformation can surely be synchronised in the time zero point and be simultaneous with the synchronised pulses of the stationary frame.

With it, different pace of time flow in the frames in no way can change such synchronisation in time; it is easy to show in the relativistic Fig. 3. To prove this assertion, let us arrange the observers with synch clocks along the time-like trajectory of moving observer, and let at the point 1 the between-frames synchronisation of clocks takes place. Then at the moment of meeting with the second stationary observer, from the view of moving frame ' seconds will pass. The clocks of stationary observers go, and at the second moving observer from the synch instant there also will pass the time interval , and the between-interval correlation at an uniform mutual speed of frames is also constant. If now we take the second moving observer and in full accordance with the first scheme locate observers along his time-like trajectory, premising that the time synchronisation occurs at once with the clocks of stationary observers, the second stationary observers will detect the meeting with the moving observers in equal time intervals. After transforming to the moving frame this will give the equal time intervals, too. Consequently, if the meetings of moving observers with those stationary at the synchronisation points are taken as the zero points of time from the view of both frames, the meetings with the second observers will be also simultaneous in each frame, as in each frame same quantity of time passed from the instant of synchronisation. We can continue this chain of events up to infinity, increasing the number of observers in the stationary frame and the number of observers in the moving frame, which will lead us to a full synchronisation of clocks between both frames, irrespectively of the pace of time in each.

In this simple technique of synchronisation, important is not that the clocks will go same in both frames but that if in one frame the clocks were synch, this automatically means mutual synchronisation of the clocks in the second frame, and this will be important for further study. And if in the sequential meetings of moving observer with that stationary the mutually passed time differs – e.g., in binary code, – this will disprove the relativistic principle of relativity. Actually, we know that according to this principle all frames are identical. From this, in the example shown in Fig. 3 we can take any frame as the stationary and from the frames identity determine that the clocks of second frame go slower. But if in each frame at the moment of meeting and exchange of time codes the observer detects that in another frame the time goes slower and in the same proportion, then in both frames time goes same and proportionality factor is 1. We can easily prove it. If from the point of stationary observer the time interval in the moving frame is

and from the point of moving observer it is

and both time intervals are real (not imaginary) in each frame, then, joining (7) and (8), yield

from which it immediately follows

If we disprove (10), we have to admit that in some frame the time really contracts and in another does not, which violates the equivalence of frames.