SELF |
58 |
S.B. Karavashkin, O.N.
Karavashkina |
|
|
|
|
|
|
|
Another
important characteristic of a wave process in a complex resistant line is the experimental
measurement of vibration velocity of the lumped line end elements or of the distributed
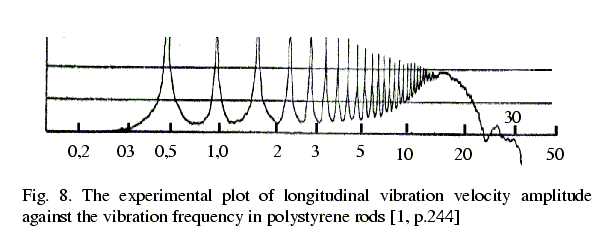
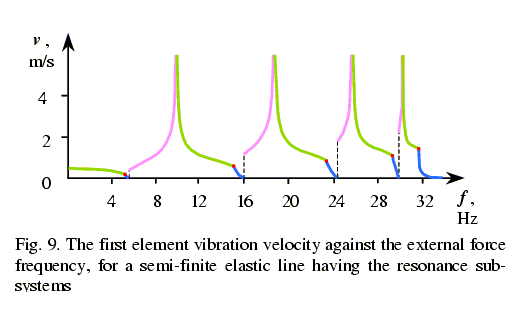
line end. Skudrzyk [1] has carried out this investigation. In Fig. 8 we show one of
regularities of the rod end vibration velocity against the frequency taken from [1,
p.244], and in Fig.9 ¢ the similar theoretical regularity, obtained by way of (9) ¢
(12) time differentiation. The difference between the theoretical and experimental results
is only in the regions of lower spikes caused by the aperiodical vibration regime. This
last is conditioned by the studied model ideality. With the line resistance appearance,
the transition between the periodical and aperiodical regimes smoothes, and damping at the
aperiodical band decreases, while at the periodical band it increases. The vibration
pattern transformation itself with the resistance appearance is very interesting and can
be studied on the basis of exact analytical solutions obtained here. However here we will
limit ourselves with the above analysis, as this investigation far exceeds the frames of
present task. Basing
on exact analytical solutions obtained for semi-finite elastic line with resonance
subsystems having the form of linear elastic lines with rigidly connected end elements, we
have revealed that between the first boundary frequency for the elastic line as a whole
and that for the subsystem the resonance peaks arise, and their quantity is equal to the
integer part of [(n ¢ 1)/2], where n is the number of elements in the
subsystem. These resonance peaks arise at the boundary between the aperiodical and complex
aperiodical vibration regimes. And this last regime is typical namely for elastic systems
having resonance subsystems. In simple elastic lines its appearance is impossible. Despite
in complex aperiodical regime the measure of inertia of a resonance subsystem is negative,
the phase delay of this process does not become leading. It fully accords with
SkudrzykÆs conclusion that the negative measure of inertia of resonance subsystem
completely corresponds to the conservation law. In this regime, with the steady-state
process in the line the standing waves form, and the wave propagation phase velocity turns
to infinity for the ideal line. We also
have determined that for interior elements of an elastic line the resonance peaks
bifurcate, and it fully corresponds to SkudrzykÆs experimental results. However the
reason of bifurcation is not the resonance circuits mismatch, as Skudrzyk supposed, but
the features of resonance peaks formation for the input resistance and transfer function
of an elastic line, which causes the resonance frequencies for these parameters to be not
the same. The
theoretically obtained regularities for vibration velocity of a boundary element of a line
are in good agreement with SkudrzykÆs experimental results. |
|
čŅõÕµÓĒĶÕ: / 48 / 49 / 50 / 51 / 52 / 53 / 54 / 55 / 56 / 57 / 58 / 59 /