т.2 No 1

69

К решению для бесконечной неоднородной линии

В первом участке распространяется прогрессивная волна со сдвигом фазы, определяемым комплексным множителем в квадратной скобке выражения (42):

Во втором участке наблюдается сложный колебательный процесс, определяемый аналогичной скобкой в выражении (43). С одной стороны, волновой процесс в этом участке обладает фазой

нелинейно зависящей от параметра x₀ . С другой стороны, амплитуда волны также нелинейно зависит от этого параметра. Её величина пропорциональна выражению

Экстремальные значения амплитуды будут достигаться в точках

где p = 0, 1, 2, ...   . В первом случае выражение (47) равно v₂ , а во втором v₁ . В зависимости от соотношения между скоростями распространения волны в соответствующих частях линии, в этих точках будут наблюдаться максимумы или минимумы волнового процесса.

Полученные для первого и второго участка результаты существенно отличаются от существующих представлений, основанных на простой суперпозиции прямой и обратной волн. Согласно этим представлениям, “амплитудный коэффициент отражения

амплитудный коэффициент пропускания

(где A₁, A₂, B₁ - соответственно амплитудные коэффициенты прямой, отражённой и прошедшей волн; Z₁ = ₀₁₁ =T / ₁ - механический импеданс первого участка упругой линии; Z₂ = ₀₂v₂ = T / v₂  - механический импеданс второго участка упругой линии - Авт.). Мы сразу видим, что эти коэффициенты не зависят от и одинаковы для волн любой частоты. Они действительны и не вносят никаких фазовых сдвигов, если не считать сдвиг на радиан, который будет изменять знак члена” [11, с. 123].

Из приведенного анализа видно, что в результате отражения от перехода неоднородности и в первой, и во второй областях образуется сложный волновой процесс, фаза и амплитуда которого будут впрямую зависеть от частоты внешней силы и от параметров упругой линии. Причём эти выводы справедливы и для прошедшей волны.

В третьем участке упругой линии наблюдается прогрессивная волна с фазой запаздывания вдоль линии, равной x₀ / v₂   и общим фазовым сдвигом, определяемым в (44) комплексной единицей и  x_k / ₁ .

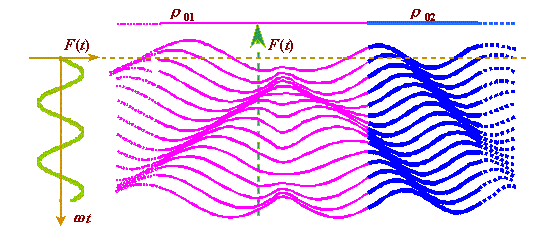
Рис. 4. Диаграмма поперечных колебаний в неоднородной упругой линии с распределенными параметрами при частоте f = 5 Гц и амплитуде F₀ = 1 Н . Параметры системы: ₀₁ = 1,7 кг / м ; ₀₁ = 4,5 кг / м ; Т = 1 Н

Чтобы представить характерную картину колебаний, удобно перейти от продольных колебаний к поперечным. Для этого достаточно направить внешнюю силу перпендикулярно оси линии и в решениях (42)- (44) заменить продольное смещение  x - x₀  поперечным смещением y . Характерная диаграмма поперечных колебаний в неоднородной упругой линии с распределёнными параметрами приведена на рис. 4. Представленная на ней картина колебательного процесса полностью подтверждает анализ решений (42)- (44), проведенный выше.