| т.2 No 2 | 5 |
| Теорема о роторе потенциального вектора | |
|
|
3. Полное доказательство теоремы о роторе потенциального вектора в динамических полях Рассмотрим некоторый
динамический поток вектора |
|
 Рис. 4. Общий вид циркуляции
вектора
|
|
Тогда длина всех трубок тока,
проходящих через объём V, будет одинакова и
для них будет справедливо соотношение между
длиной силовой трубки |
|
| (18) | |
Введём систему
координат (nr ; nn; nb),
в которой Во введенной
системе координат вектор |
|
| (19) | |
| Используя стандартное
определение (9), определим циркуляцию |
|
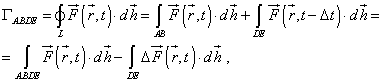 |
(20) |
| где d |
|
Как видно из (20), вследствие появления фазы запаздывания, циркуляция вектора разбилась на две части: стандартную пространственную циркуляцию вектора и интеграл, зависящий от степени запаздывания волнового процесса в пространстве. Первая часть, в отсутствие вихрей и токов, естественным образом обращается в ноль. Второй интеграл по замкнутому контуру L легко преобразуется в интеграл по площадке S, ограниченной данным контуром. Чтобы осуществить
указанное преобразование, разобьём площадку S
на p площадок вдоль направления
распространения потока. Тогда |
|
 |
(21) |
| где | |
| в данном случае 1 |
|
 |
(22) |
| Подставляя (22) в (20), получим | |
 |
(23) |