| СЕЛФ | 6 |
| С.Б. Каравашкин и О.Н. Каравашкина | |
|
|
| На основе полученного значения
циркуляции вектора можно определить ротор
потенциального динамического вектора |
|
 |
(24) |
| Поскольку в выражении (24)
скалярное произведение определяет проекцию
вектора |
|
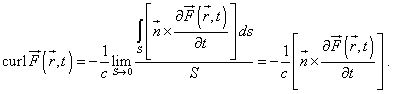 |
(25) |
Таким образом, нами в общем случае доказана теорема: ТЕОРЕМА 1: В динамических полях ротор вектора пропорционален векторному произведению единичного вектора направления распространения потока на производную от вектора потока по времени.
4. Приложение теоремы о роторе к динамическим полям В ходе доказательства теоремы о роторе вектора в динамических полях мы сознательно опустили вопрос о потенциальности исследуемого поля. И во введении, и при доказательстве теоремы мы неоднократно сталкивались с тем, что если пользоваться существующим представлением о потенциальности вектора (4), то возникает важный вопрос о трансформации потенциального вектора в соленоидальный при переходе от стационарных полей к динамическим. Причём во введении на примере акустической и электродинамической моделей показано, что два строго потенциальных динамических источника путём линейной суперпозиции способны сформировать поперечный динамический вектор поля, а следовательно, по существующему представлению, и соленоидальное поле. Чтобы детально разобраться в данном
вопросе, продолжим выкладки (6), разложив скорости
|
|
 |
(26) |
| Подставляя (26) в (6) и учитывая, что по
условию задачи v1
= v2 = v = grad |
|
| (27) | |
Из (27) следует, что вектор
результирующей скорости смещения молекул в
акустическом поперечном поле также остаётся
потенциальным, хотя и направлен перпендикулярно
направлению распространения волны, а потенциал Появление столь неожиданного результата, расходящегося со стандартными представлениями, несложно объяснить. По существующей системе рассмотрения подобных вопросов, сначала путём суперпозиции потенциальных полей формируют результирующее поле, потом, учитывая удалённость исследуемой точки от излучателя, осуществляют все необходимые упрощения. При этом путём приближений формируется единая волна с поперечным вектором, которую и анализируют для определения потенциальности поля. Мы же, записывая выражение (6), только частично произвели упрощения, сохранив условия, приведшие к формированию поперечного вектора, что нисколько не ограничило решение, но позволило более точно рассмотреть вопрос о потенциальности вектора. Ротор данного
градиента потенциала согласно доказанной
теореме уже не обратится в ноль, что не означает и
замыкания силовых линий вектора В связи с возможностью существования поперечного динамического потенциального вектора возникает вопрос о его динамических источниках и стоках – то, что послужило основанием Р.В. Полю и другим исследователям для замыкания силовых линий динамического электрического поля. Для ответа на этот вопрос обратимся к результатам работы [10]. В данной работе доказано, что дивергенция продольного вектора динамического поля не равна нулю. Но согласно существующим представлениям это может быть только в том случае, если внутри исследуемого объёма имеются нескомпенсированные заряды, которых по условию задачи там нет. Их роль выполняет само поле, вследствие своего запаздывания в пространстве. Тем самым поле сохраняет “память” об источнике в момент своего образования. Аналогично и в случае потенциального поперечного вектора. В непосредственной близости от источника потенциальность данного вектора не вызывает сомнения, поскольку для каждой точки поля всегда можно определить мгновенный источник и сток, сформировавшие данную результирующую направленность вектора поля. На больших расстояниях, когда волна отрывается от источника, поле также сохраняет “память” об источнике в момент его образования. Эта память могла бы отсутствовать только в случае, если бы скорость распространения волнового процесса была бесконечной, но тогда и правая часть выражения (25) автоматически обратилась бы в ноль, что и подтверждает вышесказанное. Кстати, и сам прогрессивный волновой процесс в пространстве при этих условиях был бы невозможен. |
|