Bend effect on vibration pattern

СЕЛФ	98
С.Б. Каравашкин и О.Н. Каравашкина

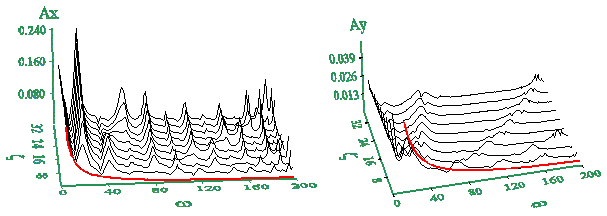
. Рис. 12. Амплитудно-частотная характеристика продольной (а) и поперечной (б) компонент колебаний в упругой линии с изломом под углом = 60^{^o}, в зависимости от отношения продольного и поперечного коэффициентов жесткости . Параметры модели: m = 0,01 кг , F₀ = 1 Н , k = 15, s_lt = 100 Н/м , = 1,0 - 37,0 , = 60^{^o}
На рис. 12 приведена амплитудно-частотная характеристика (АЧХ) продольной и поперечной компоненты волны в упругой линии до излома в зависимости от . При = 1 (ближняя кривая на графиках) АЧХ имеет нормальный для идеальных линий гиперболический вид. С ростом на графиках появляются резонансные пики, амплитуда которых растёт с увеличением . Некоторые пики в средней области частотного диапазона появляются только при больших значениях , амплитуда некоторых пиков с ростом сначала растёт, а затем сглаживается. Амплитуда пиков поперечной компоненты смещается с ростом . Это обусловлено увеличением _tr согласно (32). Характерно, что, несмотря на идеальный характер упругих связей, амплитуды резонансных пиков конечны. Расположение пиков для продольной и поперечной компонент колебаний также не совпадает. В связи с этим, в линиях подобного типа в зависимости от частоты могут преобладать продольные или поперечные колебания. Таким образом, при распространении волны со сложным и особенно непрерывным спектром, который характерен для уединённых сейсмических волн, будет происходить существенная трансформация формы волны. Ряд частот в процессе распространения будет подавлен, а на ряде частот, соответствующих резонансным пикам, амплитуда колебаний резко возрастёт и этот процесс не будет синхронным для продольной и поперечной компонент. К этому добавится процесс размывания волнового пакета, обусловленный зависимостью фазы запаздывания (а значит, и скорости распространения) от частоты. Учитывая же, что в области до излома имеет место сложная суперпозиция стоячей и прогрессивной волн, дисперсия скорости будет нелинейно зависеть от частоты внешнего возбуждения.
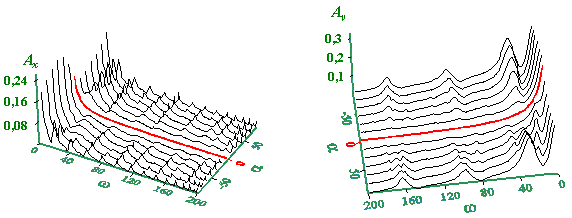
a b Рис. 13. Амплитудно-частотная характеристика продольной (а) и поперечной (б) компонент колебаний в упругой линии с различными продольным и поперечным коэффициентами жесткости в зависимости от угла излома , отношения . Параметры модели: m = 0,01 кг , F₀ = 1 Н , k = 15, s_lt = 100 Н/м , = 10 , = 60^{^o}
Подобная картина наблюдается и для АЧХ в зависимости от угла излома упругой линии, графики которых для продольной и поперечной компонент в области до излома приведены на рис. 13. При = 0 (кривая в средней части графиков) АЧХ также будет иметь стандартный для идеальной линии гиперболический вид даже при > 1. С ростом на АЧХ будут возникать резонансные пики, амплитуда которых будет возрастать с ростом и их характер будет зависеть не только от величины, но и от знака . Применительно к сейсмическим процессам это означает, что чем резче переход от равнинного ландшафта к горному а также чем резче изгиб горной дуги (характерным примером является Памирский узел), тем разрушительнее последствия землетрясения. Как и на рис. 12, скорость роста амплитуды будет различной для разных пиков. Некоторые пики будут проявляться только при больших значениях , низкочастотный пик на рис. 13 б с ростом сливается со следующим резонансным пиком и положение пиков на АЧХ продольной и поперечной компонент будет не совпадать.