т.2 No 1

79

Некоторые особенности моделирования вынужденных колебаний

К сожалению, ни в практических исследованиях (см. напр. [16], [6]), ни в фундаментальных исследованиях на базе интегральных уравнений (см. напр. [11], [12]) этот режим колебаний не рассматривается и не учитывается. “Решение краевых задач теории колебаний сводится, по существу, к определению собственных значений, связанных с собственными частотами или другими параметрами исследуемой системы и нахождению собственных функций (форм колебаний). Если собственные значения и собственные функции найдены, тогда можно считать краевую задачу решенной… В настоящее время разработано большое число приближенных методов нахождения собственных значений, но все они довольно трудоемки, позволяют находить только первые собственные значения и, главное, не объединяют изучение систем с дискретным и непрерывным распределением масс. Потому, как справедливо считают многие авторы, определение собственных значений до настоящего времени является одной из наиболее важных и вместе с тем наиболее трудоемких задач, которой продолжают уделять внимание исследователи, в том числе Келлатц, Гулд, Уилкинсон в вышедших в последнее время фундаментальных монографиях, посвященных проблемам собственных колебаний. Вопросы установления математического единства и синтеза одномерных дискретных и непрерывных граничных задач рассматривались еще в работах Эйлера и Лагранжа. Однако и до настоящего времени продолжается установление аналогий между такими граничными задачами, например, в работах Крейна, Аткинсона и др.” [11, с. 3- 4].

С точки зрения нового аналитического метода, можно образно объяснить проблему собственных значений высшего порядка, используя модель, состоящую из трех участков упруго соединенных масс. Если первые k₁ тел имеют массу элементов m₁ , вторые k₂ тел имеют массу m₂ > m₁ и остальные (n - k₁ - k₂) k₁ тел - снова m₁, то при собственных частотах, докритических для всех секций, каждому участку будут соответствовать собственные значения резонансных частот, трансформированных взаимным влиянием участков. При частотах, закритических для "тяжелого" участка, линия четко разделяется на три области. В первой и третьей будет сохраняться периодический колебательный режим, а во второй - апериодический. Если колебания будут свободными, можно ожидать "частичные" резонансы в каждом из трех участков - в двух в докритической области и в третьем участке - в закритической области. Но если колебания вынужденные, то решения будут зависеть от точки приложения внешней силы.

Поэтому, описывая линию унифицированной матрицей общего вида и не принимая во внимание возможные переходы в некоторых участках (или отдельных массах) к апериодическому режиму, мы при описании процессов в линии естественно натолкнемся на непреодолимые проблемы. И то, что ни матричный метод, ни метод интегральных уравнений не выявляют закритического режима колебаний, свидетельствует только о некоторой неполноте этих методов и необходимости развития и принятия во внимание особенностей колебательного процесса. Новый нематричный метод также может быть полезен в этом. Некоторые результаты, полученные с его помощью, были представлены в [1]- [3], и решения, анализируемые в этой статье, были также получены данным методом.

3. Влияние точки приложения внешней силы

3.1. Конечная линия с незакрепленными концами

Для удобства сопоставления с решениями, приведенными в работе [1], рассмотрим конечную линию с незакрепленными концами, на k–й элемент которой (1 k n ) воздействует внешняя гармоническая сила. Общий вид данной линии приведен на рис. 1.

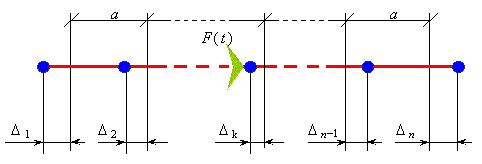
Рис. 1. Общий вид конечной упругой линии, на k-й элемент которой воздействует внешняя сила

Моделирующая система уравнений имеет вид:

где F(t) = F₀ - внешняя сила, воздействующая на k-й элемент линии, m - масса элемента линии, s - коэффициент жесткости связи, _i - мгновенный сдвиг i-го элемента из состояния покоя.