V.6 No 1 |
55 |
| The problem of physical time in today physics | |
|
|
V.6 No 1 |
55 |
| The problem of physical time in today physics | |
|
|
3. The features of light propagation in the mutually moving inertial reference frames from the view of classical physics In the previous section we showed the dynamic diagram of propagation of the wave of light from the resting source in the resting reference frame. Now let us see this pattern from the point of frame mowing along the resting frame with the speed v in direction of positive values of the axis x. We will begin from the classical representation. Suddenly it will appear that we can do such transitions from one frame to another in two different ways. The simplest way is to transform coordinates immediately from the resting frame to that moving. Going this way, we will proceed from a trivial understanding that in the resting inertial frame for the resting source located at the coordinate origin, the equation of arbitrarily chosen equiphase surface is |
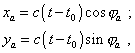 |
(3.1) |
where xa , ya are the coordinates of momentary location of points of
equiphase surface in space, Supposing that at the initial moment of time t = t' = 0 the origins of moving and resting frames coincide, and noting the usual for classical physics transformation of coordinates between the inertial frames, |
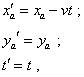 |
(3.2) |
where x'a , y'a are the coordinates of momentary location of the points of equiphase surface in the moving frame, v is the speed of coordinate system’s motion, – we yield the equation for the equiphase surface from the point of moving frame as |
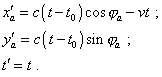 |
(3.3) |
The dynamic diagram for these modelling equations is shown in Fig. 3.1. |
Fig. 3.1. Dynamic diagram of propagation of the light equiphase surfaces from the point of inertial frame moving with the speed v = 0,8 c with the positive values of x of the resting frame when direct passing from the resting to moving frame in classical formalism. The diagram was plotted for the times from t0 = 0 to t0 = 6T, where t0 is the moment when the equiphase surface was radiated; the world line of the observer is denoted in blue
|
We see from this diagram that the classical passing retains the plane of events between the inertial frames, which shows, in this case the classical formalism corresponds to the condition at which the physical time has been introduced in both frames. We also see something unusual in the distribution of equiphase surfaces. We used to think the processes of wave propagation from the moving source so that at the wave front the equiphase surfaces are concentrated and behind the source – rarefied. In the diagram this is absent. To understand, why, imagine that some frame moves over the water surface and the source of surface waves is in the water. As the source rests with respect to water, the waves are formed in relation to water as the concentric rings that propagate from the source. By the very meaning of passing from one frame to another, all points of resting frame are synchronously mapped into the points of moving frame, so in this last we will see not the deformation of rings but only their synchronous shift in time, in direction opposite to the motion of frame – and the diagram shows it. This does not mean that the Doppler effect disappears in
this transition. To show it, consider, how the period between two sequential equiphase
surfaces is transformed in passing from the resting to moving frame. Suppose, as in the
diagram, that the observer is at the point (x1, 0, 0) of moving
frame; hence, for this location of observer |
| (3.4) |
Then, let the source radiate the next equiphase surface at the moment t0 + T , where T is the between-pulses period in the resting frame. This equiphase surface will reach the observer at the moment t1 + T ' , where T ' is the between-pulses period in the moving frame. As the observer rests in his frame, the time when the second equiphase surface arrives will be |
| (3.5) |
Subtracting (3.4) from (3.5) and making simple transformation, yield |
| (3.6) |
or for frequencies |
| (3.7) |
where we take plus with the source approaching the observer in the moving frame, and minus – with the source moving off. The yielded expressions (3.6) and (3.7) show that for
moving observer the between-pulses period changes after the same regularity as Doppler law
for the longitudinal case [15, p. 49]. True, in the Doppler law the ratio of speeds in the
right part is inverse, c/(c At this stage of our study we can see: when direct passing from one frame to another, the classical formalism does not distort the equiphase surfaces, but the moving observer detects the transformed signal, because of change of distance between the source and observer, when receiving sequential pulses from the source. The equiphase surfaces are kept from distortion because in this case the medium (in case of hydrodynamic or mechanical waves) or aether (in case of EM waves) moves with the source as the whole in relation to the observer. And only the complete plot of equiphase surfaces shows the absence of their real transformations. Here we encounter the features of relative measurement and absolute comprehension and generalisation of which Newton said. Doing specific measurements of period or frequency, we will detect their transformation, and the plotted patterns will contain these particular results of measurement. But if we detect the wave simultaneously at different points of moving frame, we will see non-transformed equiphase lines; this will reflect the physical reality non-limited by distortions of perception. We easily can make sure that this generalisation is just the transition from particular perception to the physical reality, if we note that on the basis of shifting sequence of equiphase surfaces we can yield our particular result of measurements, but basing on the particular result of measurements of one observer, we cannot catch the feature of synchronous shift of equiphase surfaces in space. This is typical between the particular and general, when we can easily pass from the general to particular, but it is impossible to pass from the particular to general, as in the particular usually are absent some properties that reveal themselves in other particularities of this general but are not revealed in this particular. We will see it when considering the second way to pass from the resting frame to that moving. |
Contents: / 53 / 54 / 55 / 56 / 57 / 58 / 59 / 60 / 61 / 62 / 63 / 64 / 65 / 66 / 67 / 68 / 69 / 70 / 71 / 72 / 73 / 74 / 75 / 76 / 77 / 78 / 79 / 80 / 81 / 82 / 83 /