V.6 No 1 |
73 |
| The problem of physical time in today physics | |
|
|
V.6 No 1 |
73 |
| The problem of physical time in today physics | |
|
|
6.4.2.3. The features of revelation of inertial forces in a freely falling reference frame in a homogeneous gravity field As we showed in the previous subsections, the phenomenology of physical processes in non-inertial frames generally does not corroborate the hypotheses which Einstein has put forward to substantiate the general theory of relativity. And if Einstein based on some premises, we can surely say, he built his premises namely on the regularities that reveal themselves in the homogeneous field of acceleration, and regularities described not from the view of relativistic conception but just on the basis of classical formalism. To show it, consider from two points of view – relativistic and classical – a trivial problem of some amount of masses in an external homogeneous field of gravity, how the conservation laws work in passing from the inertial frame to that non-inertial that falls in this field together with masses. Begin with the classical representation. Let in some
region of space that is under affection of a homogeneous gravity field, there is located
some compact amount n of masses mi , i = 1. 2, 3,
... , n each of which at the initial moment of time t0
has the velocity |
| (6.34) |
then in S |
| (6.35) |
Noting that from the view of classical physics |
| (6.36) |
we yield from (6.35) |
| (6.37) |
Thus, if in one frame the law of impulse conservation |
| (6.38) |
is true, where 1 and 2 denote the sum of impulses before and after some process occurring in this frame, then in the another frame, according to (6.36), the equality |
| (6.39) |
will be true, too. Since on one hand |
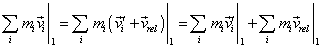 |
and on the other |
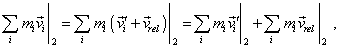 |
joining the yielded expressions gives (6.39). Similarly, from the point of classical physics, we, basing on the energy conservation law, may not select a non-inertial frame being in the homogeneous field of mass forces. To show it, consider the same amount of n masses. Let the total kinetic energy of the amount of bodies, before some interaction in the resting frame S be equal |
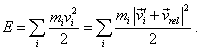 |
(6.40) |
In passing from one frame to another, in classical physics
we vectorially subtract the velocity of frame having the same value |
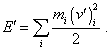 |
(6.41) |
From (6.40) and (6.41) it automatically follows that if in one frame the energy conservation law was true, then, noting that all bodies of the studied amount have an additional velocity together with frame S' , in the moving frame the energy conservation law will remain. Actually, let in the resting frame the energy conservation law is true; then we may write |
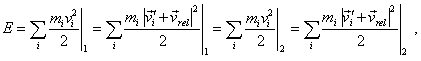 |
(6.42) |
where, as before, 1 and 2 mean the total energy of the system before and after some process. In (6.42) we can transform the left part as follows: |
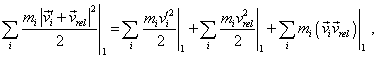 |
(6.43) |
and the right part, relatively: |
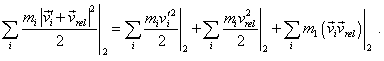 |
(6.44) |
Now, to yield from (6.43) and (6.44) the energy equation for the moving frame, we only have to account that the second summands in the right parts of these expressions are equal and the third summands are equal, which follows from the conservation of the impulse of system. So we yield |
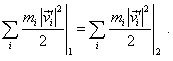 |
(6.45) |
We also see from (6.43) and (6.44) that if in passing from one frame to another the law of impulse conservation is not true, the law of energy conservation will be untrue, too, as the situation is impossible when in some formalism one conservation law is true and another is not. Both laws must be true or not. It also follows from our consideration that in the inhomogeneous gravity field, in passing between the inertial and non-inertial frames, the conservation laws will not be in such agreement with each other, as each of considered bodies will have its own acceleration of free fall proportional to the strength of gravity field at the place of location of this body. As the value of this acceleration for separate bodies will not be same as the acceleration of the frame’s origin, in (6.39) and (6.45) the non-compensated summands will appear, and they will make the frames non-equivalent. And in the relativistic formalism this correspondence, even approximate and even in the homogeneous gravity field, is not true. We can easily make sure of it if we consider the same conservation laws for impulse and energy in limits of this conception. Let us begin with the conservation law of impulse of the system of bodies. The law of impulse conservation to remain true in passing from one frame to another, two conditions have to be satisfied: – the conservation law has to be true in the initial frame; – the transforms have to remain the parallelogram law. The Lorentz transforms and Einsteinian kinematics satisfy neither. Actually, let at some, even inertial, frame some amount of bodies moves arbitrarily and their trajectories cross each other in extrapolation, which implies interaction between these bodies. And let the total impulse before the interaction be |
| (6.46) |
“Relativistic mechanics proceeds from the premise that in the coordinate system K' , in which the material point is resting at the considered moment, the following equations of motion of old mechanics are true: |
| (6.47) |
[23, p. 170]. It immediately follows from this that if at the next moment of time the material body has gained the speed (which is predestined by the equations of motion (6.47)), then (6.47) is already untrue. Nothing to say of considered problem where we consider some amount of material bodies moving with different speeds which we cannot think resting in this frame even at the initial moment. Really, “… introducing the hypothesis that the mass mv depends on the energy, which means – also on time, we encounter the difficulty that for this case the equations of mechanics are already unknown; the first equality in the relationship |
| (6.48) |
is already untrue. None the less, we have to assume that the difference |
| (6.49) |
is in proportion to the second order of speed. So, if all speeds are so little that we can neglect the second-order terms, in the change of mass mv the equation |
| (6.50) |
remains true with the assumed accuracy” [77, p. 43]. Like this, Einstein solves the problem with the change of
time in uniformly accelerated frames: “First of all we have to
account that we can neglect the specific affection of acceleration onto the pace of clocks
We know that the negligible smallness of quadratic terms corresponds, from the relativistic viewpoint, to the area in which classical mechanics is true and in it the conservation laws are true without the hypothesis in which the mass depends on the energy of body, and out of this area the laws of mechanics are not true. So we may surely state that in frames of SRT that describes, from the relativistic view, just the motion of bodies whose speed is comparable with that of light, we may not speak at all of the dynamic equivalence of frames. And not only inertial frames but non-inertial, too. It follows from the said that we may not consider in the relativistic conception any dynamic transforms, in that number on the basis of Maxwell theory. Not better things are with the coordinate transform. If we state the problem so as we stated it before, in case of classical formalism, namely – passing from the inertial frame to that non-inertial, we will find this passing non-obvious in the relativistic formalism, as it is not clear a priori, whether the postulate of lightspeed constancy will remain true in the non-inertial frame. And Einstein tried to substantiate that we may apply SRT to the non-inertial frames as follows: “We still applied the principle of relativity, i.e. the requirement, the laws of nature to be independent of the state of frame’s motion, only to the non-accelerated frames. Can we imagine that the principle of relativity is true also for frames moving relative to each other with an acceleration? True, we still have not a possibility to discuss here this question in details. But as this question has to arise before each who followed how we applied the principle of relativity up to now, I will express my opinion on this matter. Consider two frames We know that the physical laws related to This premise extends the principle of relativity onto the case of uniform rectilinear motion of the frame” [52, p. 105–106]. As we see, this substantiation is only an attempt to prove
the statement through the corollary of the same statement. Well, to have a right to write “We know that the physical laws related to The situation in relativity is even worse because in fact Einstein was not interested in the gravity field as such. To build the general theory of relativity, he had an inhomogeneous field. Recall the technique, how Bergmann calculated the curve of space-time, going round the closed time-like loop that we analysed in the section 5. If on the sides of this loop the acceleration of free fall is same, then the curvature of space-time will be zero, irrespectively of, whether the frame is accelerated or not. And only with the difference of free-fall acceleration in the path-tracing there arises some resulting inclination of vector which we can attribute to the curvature of space. But this means that the falling frame has to move in the inhomogeneous gravity field. As we showed above, in such field the equivalence will not take place; as the consequence, it will transform the shape of the system of bodies whose different parts will be affected by the mass force different in amplitude. And namely understanding that the laws of dynamics are violated in non-uniformly accelerated frames stimulated Einstein to introduce the equivalence within the uniformly accelerated frame and to apply it to the non-uniformly accelerated frames, which additionally made GRT an artificial abstract theory. At the same time, using the evidence that we yielded above – that material points and field processes are transformed differently even within the classical theory, and differently just in the meaning that, since the field processes are interconnected with the luminiferous substance, even inertial frames appear non-equivalent, – we can extend our conclusions made in the previous sections and show that in the freely falling frame it is senseless to speak of constant speed of light even in frames of classical formalism, nothing to say – to postulate this constancy within the relativistic formalism. Since this consideration is exceptionally important for the studied issue of equivalence of reference frames, we will enlighten it in a separate subsection. |
Contents: / 53 / 54 / 55 / 56 / 57 / 58 / 59 / 60 / 61 / 62 / 63 / 64 / 65 / 66 / 67 / 68 / 69 / 70 / 71 / 72 / 73 / 74 / 75 / 76 / 77 / 78 / 79 / 80 / 81 / 82 / 83 /