V.6 No 1 |
79 |
| The problem of physical time in today physics | |
|
|
V.6 No 1 |
79 |
| The problem of physical time in today physics | |
|
|
Now we can undertake more targeted study of intervals transform, premising that, if this phenomenon relates to the phenomenology, we will be basically unable to transmit a non-distorted time interval from one frame to another. But if the transformation of intervals follows from systematics of measurement, then on one hand, this is already the problem not of fundamental physics but of theoretical metrology, and on the other, it does not relate to the space-time transform on whose basis relativists build their conception. To answer this question, we will some more complicate the considered scheme of synchronisation, using a trivial metrological technique excluding the systematic errors of measurement “in which the measurements are done twice, so that the error was included into the measurements with different signs” [82, p. 20]. With it, we will proceed from the fact that if applying the trivial scheme of compensation of systematic errors, we do not eliminate the transformation, this will mean the phenomenological essence of the phenomenon of transformation of time intervals. In the opposite case, i.e. if the transformation of time intervals disappears, we should relate the difficulties to the fundamental metrology and ignore them in modelling of processes in fundamental physics. Now consider a simple scheme; it consists of three
identical frames. Einstein also applied a similar scheme to prove the Lorentz transforms: “it (the function In distinct from the described Einstein’s scheme, suppose that the speed of third frame S is equal to a half of mutual speed of frames S' and S'' (from the point of observer in S). Furthermore, as we are free in choice of resting frame, let us take the frame S as the resting one, and according to the model considered in Fig. 7.2, let us put the marks synchronising the time intervals for each frame, both S' and S'' . So we will yield the model shown in Fig. 7.3. |
Fig. 7.3. Scheme of clocks synchronisation in the mutually moving frames S' and S'' with the help of auxiliary inertial frame S
|
In this figure we see a symmetrical scheme of motion of the frames S' and S'' relative to S. Naturally, we can set the markers so that from the point of frame S both moving frames coincide with their first markers B and G at the same time, i.e. |
| (7.41) |
Now, with the technique of solving of the previous problem, we will sequentially find the periods of synched time in frames S' and S'' . Basing on the Lorentz transform, find the moment when the clock A meets the marker B as |
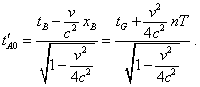 |
(7.42) |
The value of time interval in the frame S' we can write with (7.38): |
| (7.43) |
Similarly, we can yield t''F0 and T'' for the frame S'' : |
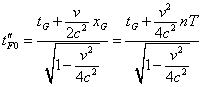 |
(7.44) |
and |
| (7.45) |
From these formulas it follows that |
| (7.46) |
and from |
| (7.47) |
it follows that |
| (7.48) |
Finally, it is easy to show that when S' and S'' meet at the point O, their synched clocks will read same time. Actually, at the given point |
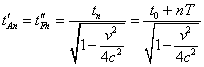 |
(7.49) |
and the time intervals from the coincidence of points B and G to the coincidence with the point O are |
| (7.50) |
Thus, we, doing not exceeding the limits of Relativity, proved that in the studied mutually moving frames, both unit intervals and current times are equal; consequently, the relativistic time transform is imaginary and can be the subject of study of theoretical metrology, not of fundamental physics. Additionally we have to mark, the analysis of Fig. 7.2 and 7.3 can show the full absurd of involving of time transforms into the formulas for coordinate transform. Now let us look at the expression (7.36) for Fig. 7.2 and (7.42) and (7.44) for Fig. 7.3. They describe the moment of time which the moving observer detects in synching the clocks when meets the first marker of resting frame. As is given, the marker passes to the moving observers not only a synched impulse but the code of current time in the resting frame. The Galilean transforms fully describe this feature, joining the times of both frames, so we have no difficulty with further transformation because of it. The relativistic transforms relate the time of one frame to the basically other time in another frame, despite the code – for example, binary – cannot voluntarily change the information, because of presence of the frame’s speed. In this connection, let us ponder. Some frame with a clock in it is moving. Before it meets the first marker, its time, after the statement of problem, is not synched – it means, we can take that before synchronisation the detection of time was absent. The moving and resting frames could separate at an arbitrary moment of time. Why when meeting, the moving clock shows just the reading of time which does not catch the separation moment? If the initial reading of current time is set when the clocks coincide with the first marker, nothing to say of any prehistory of time flow. On the other hand, if, suppose, the prehistory showed itself at the moment of time synchronisation, then, noting that the time intervals in the separated frames are different and before separation, say, the time reading was same on both clocks, then it would be natural that when the clock meets marker, we would see a full difference in the current time from the moment of separation to the moment of meeting. But we see no such information in the above formulas. So the fact of attributing to the moving clock some abstract time when the marker shows a specific value of time is absurd and shows the Lorentz transforms incorrect, additionally corroborating the above conclusions that Einstein’s principle of relativity is irrelevant to the factual necessity to introduce non-equivalence of frames if one of them was accelerated. And concluding so, we already draw our attention that separation of frames takes no part in substantiation of Lorentz transforms nor in transforms themselves. In the considered problems we simply got an additional corroboration of this conclusion, showing that in the relativistic conception, the time is really detected, but it can be substantiated by no physical phenomenon, by no formal logic. This proves that the time transformation in the Lorentz transforms is not only fictitious but incorrect, as it follows from the ungrounded postulate that brings the imaginary deformations which relativists take as the transformation of space-time, while factually they are an illegal inclination of the plane of events making wrong both postulates and their corollaries. |
Contents: / 53 / 54 / 55 / 56 / 57 / 58 / 59 / 60 / 61 / 62 / 63 / 64 / 65 / 66 / 67 / 68 / 69 / 70 / 71 / 72 / 73 / 74 / 75 / 76 / 77 / 78 / 79 / 80 / 81 / 82 / 83 /