V.6 No 1 |
59 |
| The problem of physical time in today physics | |
|
|
V.6 No 1 |
59 |
| The problem of physical time in today physics | |
|
|
And we can show the main property of solutions (4.10), transforming the last parameter
of the undotted frame – the polar angle |
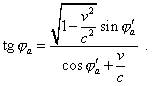 |
(4.15) |
For further computations, we can conveniently represent (4.15) as |
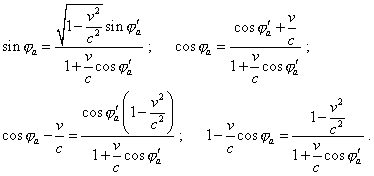 |
(4.16) |
Substituting (4.16) into (4.14), yield |
| (4.17) |
and substituting (4.16) into the expression for y'a in (4.10), yield |
| (4.18) |
If we now compare (4.17) and (4.18) with the above
modelling equations (3.8) describing
the equiphase surfaces radiated by the source moving with respect to the inertial frame,
we will see them fully corresponding to each other. To reveal finally the features of this
transform, let us complicate the problem additionally and premise that the source radiates
the wave inhomogeneous in the polar angle |
| (4.19) |
The dynamic diagram plotted with the joint system (4.10) and (4.19) is shown in Fig. 4.3.
|
Fig. 4.3. Propagation of the equiphase surfaces of the
source moving with the speed v = - 0,8 c with respect to the dotted
frame (x', y') whose intensity varies with the angle
|
As we can see from this plot, in the relativistic conception the wave propagates not with the angle behind, as classical physics predicts (see Fig. 4.4).
|
Fig. 4.4. Propagation of the equiphase surfaces of the
source moving with the speed v = - 0,8 c with respect to the dotted
frame (x', y') whose intensity varies with the angle
|
In the relativistic conception the line of minimal radiation is in one direct with the momentary location of source; it is well seen in Fig. 4.5a where we plotted a selected equiphase surface. To compare, in Fig. 4.5b we gave the appearance of equiphase surface in classical wave physics.
|
a b Fig. 4.5. An equiphase surface produced by the moving source calculated with the modelling equation (4.10) (a) and with classical wave physics (b)
|
The thickness of line in these plots is in proportion with the intensity of radiation, and we see that, actually, the minimal intensity in Fig. 4.5a is shifted towards the source’s motion, its front is compressed and rear is stretched. As this surface is the momentary location of equiphase values of intensity of the light wave, such shift of the zero values in direction with the motion evidences that in the relativistic formalism the wave process of light propagation is related to the state of source’s motion – and this contradicts the statement of problem of the relativistic conception which stated that “the light in the void always propagates with the speed V independent of the state of motion of the source” [4, p. 7, italics is ours]. The speed of light, as we saw, actually does not depend, but the distribution of the force lines in the polar angle depends; this means, the pattern of light propagation on the whole depends in the relativistic conception on the state of source’s motion, and depends in a quite strange way. On the other hand, if we, remaining in frames of relativistic formalism, plot the dynamic pattern with the modelling equations (4.17) and (4.18) which coincide with the classical expressions (3.8), but in accordance with (4.16) account additionally the transformation of angles in the expression for the radiation intensity (4.19), we will yield a full analogue of the Fig. 4.3. Doing not analysing still, how much legal is such approach and how much legal is the asymmetric transformation of the local physical time of the mutually moving frames determined by (4.6), we at this stage can state that, according to the relativistic formalism, the modelling equations that describe the equiphase surfaces radiated by the source resting with respect to the inertial frame and that correspond to the equations (3.1) of classical formalism are one-valuedly transformed into the modelling equations describing the equiphase surfaces radiated by the source moving with respect to the inertial frame in correspondence with the equations (3.8) of classical formalism. Now, do generalise this derivation, it would be of interest to consider, whether this correspondence will remain in the Lorentz transforms from the frame in which the source moves to the frame accompanying this source. Now the dotted frame S' with respect to which the source moves will be at rest, and undotted frame S accompanying the source of light will be the moving frame. With it, (3.15) will be the initial modelling equations describing the equiphase surfaces of light from the moving source in general appearance. Substituting them to the trivial Lorentz transforms (4.1), yield |
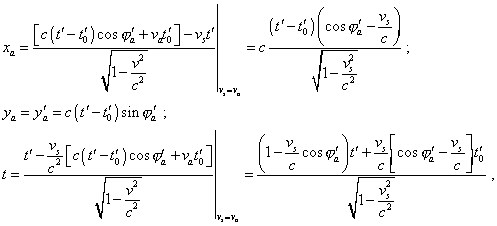 |
(4.20) |
where va is the speed of source in the frame S' , vs is the speed of frame S accompanying the source with respect to the resting frame S' . The dynamic diagram plotted with the system (4.20) is shown in Fig. 4.6. |
Fig. 4.6. Dynamic diagram of equiphase surfaces propagating from the resting source in the frame S yielded with (4.20); the speed of source in the frame S' is va = vs = - 0,8 c
|
In the plot we see the same salient features to which we drew the Reader’s attention describing Fig. 4.1. The diagram is arranged on the inclined plane and remains the asymmetric configuration of equiphase lines of the initial frame which we could see in the section 3, Fig. 3.2 . In this case, the configuration remains typical for the model of source moving with respect to the inertial frame taken as the stationary. But this does not mean that the pattern will remain when we agree the solution with the local physical time of the undotted frame. In the previous case, when we transformed the pattern of equiphase surfaces produced by the resting source, we after application of the Lorentz transforms yielded the analogue of classical case, too, only with the inclined plane of events. But when we agreed it with the local physical time, the pattern basically changed. Most likely, this will take place in the case under consideration, too. To make sure, let us agree the system (4.20) with the local physical time of the frame S , as we did it above. First of all let us determine the regularity of moments of radiation of equiphase surfaces. At t' = t'0 the condition t = t0 is true; hence, from (4.20) we have |
| (4.21) |
As we can see, given we changed the pattern of motion of the frames, remaining the dots, (4.21) coincides with (4.4). This evidences that going the reverse way, we yield the same regularities, despite we changed the way of motion of frames. Then, substituting (4.21) into the last equation of (4.20), we yield after transformations |
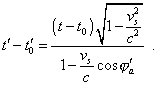 |
(4.22) |
Finally, substituting (4.22) into the first and second expressions of (4.20) for xa and ya , yield |
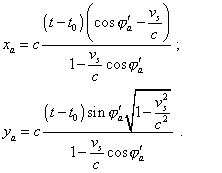 |
(4.23) |
To finish with the transforms, we have to pass from the dotted polar angle to that undotted. Noting, we consider the dotted frame as resting, we can use for this passing the above relativistic regularities (4.15) and (4.16), substituting the dotted polar angles by those undotted and vice versa. Substituting the result of this to (4.23), yield |
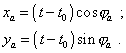 |
(4.24) |
So we came to the expected result. The expressions (4.24) fully coincide with the classical modelling system of equations (3.1) that describes the equiphase surfaces produced by the resting source. Because of full coincidence, it would be senseless to plot here the dynamic diagram of the pattern of equiphase surfaces, as it fully coincides with the above diagram of Fig. 1.1 , only the intensity of radiation will be deformed, just as in Fig. 4.3, but this deformation in frames of relativistic formalism will be natural, noting the transform of angles. Basing on the analysed main transforms of field processes in frames of relativistic formalism, we can definitively conclude that in frames of relativistic transforms, when agreeing the solutions with the local physical time of frames, we transform the dynamic pattern of the moving source with asymmetric arrangement of equiphase surfaces into the dynamic pattern of resting source with concentric arrangement of equiphase surfaces and vice versa. |
Contents: / 53 / 54 / 55 / 56 / 57 / 58 / 59 / 60 / 61 / 62 / 63 / 64 / 65 / 66 / 67 / 68 / 69 / 70 / 71 / 72 / 73 / 74 / 75 / 76 / 77 / 78 / 79 / 80 / 81 / 82 / 83 /