SELF |
78 |
S.B. Karavashkin and O.N. Karavashkina |
|
|
|
SELF |
78 |
S.B. Karavashkin and O.N. Karavashkina |
|
|
|
7.1.4. Check for correctness of relativistic time transform equation Above we showed that relativists do not derive the time transform but yield as one of corollaries of the fact that Lorentz transforms satisfy some abstract invariant that follows from the lightspeed constancy in all inertial frames. On the other hand, we know that some statement can be taken as the basis of physical conception only if it is associative with the observed phenomena. In this meaning the question, whether the contraction is real, becomes nearly main. Actually, if the time contraction is real, then, irrespectively of the measurement technique, the result has to be comparable. But if the time contraction has been caused by some side phenomena – such as the Doppler effect, deformation of particular material measures, – we may speak of systematics of particular measurement techniques, not of the global change of time pace related to the speed of frame. As the corollaries of two approaches are different, the same different have to be conclusions from our decision. If the contractions are the metrological errors, we have to reveal them and to account in measurements. If the time contraction is phenomenological, we have to put it into the description of processes in physical theories. From this view, let us return to the initial derivations by Marder and Einstein and try to find the degree of time interval transformation in the moving frame, premising the postulate of lightspeed constancy to be true. We naturally have to yield all above remarks to the shown formulas. Consider two inertial frames mutually moving with the speed v; we will think S as the resting and S' as the moving frame. Let it moves in the +x direction of S. The clock which we will further denote with the index A is located in the coordinate origin of S' , so its location is determined by the spatial coordinates x' = y' = z' = 0. Noting that the Lorentz transforms have to describe the trajectory namely for the point A from the point of two frames, their general appearance will be |
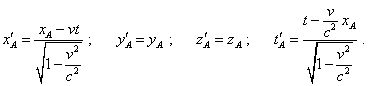 |
(7.31) |
Note, in (7.31) we did not identify the time in the resting frame, thinking that we synch not two clocks in resting and moving frames but the trajectory of the body A is described in physical time by the parameters of unprimed frame. Now find the clock’s location in its own (primed) frame and write (7.31) for some moment of time t1 of the resting frame. The transform will be such: |
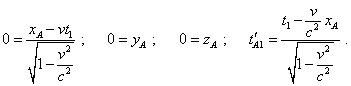 |
(7.32) |
Solving the system (7.32) with respect to t'A1 , yield |
| (7.33) |
The same for the moment of time t2 of the resting frame: |
| (7.34) |
Subtracting (7.33) from (7.34), yield |
| (7.35) |
The expression (7.35) shows that from the view of
Relativity, the time interval in the moving frame really will differ; true, it will be
shorter, not longer as Einstein thought – this means, the clock will go faster. And
given the features of frame-to-frame transform formulas, the time interval Here the feature of transforms of which we said in the subsection 7.1.2 is revealed. When we have some description of body’s motion in one frame which we took as resting and, using the transform equations, find the trajectory of body’s motion in the moving frame, – only then we find the real change of the pattern of trajectory in frame-to-frame passing, and in case of relativistic transforms also real (as it is thought in this conception) time transform. Now let us try to model these transforms on a particular model. But first let us think: what is it – the measuring time interval in the relative measurements? To answer, make use of the problem of train on which Einstein liked to demonstrate the relative effects. Let us glue up the window of compartment, retaining a narrow split; on the poles we will fix the lanterns radiating narrow beams of light. Then, sitting in the compartment of this uniformly moving train, we will periodically see the light of lanterns passing the split. Further, let us take the metronome and synch the fact of appearing light with its beats; we will yield some synched periodic process. Even when the poles with lanterns are over, we still can use for our purposes these intervals that metronome will beat. And if in some time the poles with lanterns appear again in their sequence and throw the beams of light through the split to our compartment, the periodicity will still remain – of course, if the periodicity of lanterns and speed of train remain. This means, until the state of frame remains and the conditions of transmission of etalon of period remain, the measure of unity of time interval will remain unchanged and synchronised. Not so much important where from have we got the etalon periodicity. Will it be a metronome in the train or periodically seen lanterns in another reference frame – for the observer in the train they can equally serve as the unit of relative time. So the issue of choice of source of synch of time intervals is clear, but there remains the question, how can we transmit correctly the synching intervals of time. In fact, just it defines, whether the relativistic time transformation is the problem of metrology of measurements either the phenomenological matter. Consider the scheme in Fig. 7.2. |
Fig. 7.2. The scheme of time synchronisation
|
In this scheme we see again two mutually moving frames;
the primed frame moves relative to that unprimed with the speed v in direction with
+ x. Additionally, in the resting frame we now have three marks B, C
and D which the clock A sequentially passes. We arrange these marks,
proceeding from the condition that at the moment when clock coincides with B, the
clock receives the first synchroimpulse, similar to that which the observer in the
compartment receives when the light of first lantern passes through the split. With it the
clock receive the coded information of momentary value of physical time in the resting
frame. Besides, noting that the resting observer can measure the speed of motion of clock A
before synchronisation, he puts the marks so that the distance between marks is
proportional to the unit interval T = When the clock coincides with the second mark C, the clock receives the second synchroimpulse and then count the time, basing on the received time interval, adding the values of intervals to the yielded value of current time. At the point D the current time at the resting frame is compared with the current time count by the clock in the moving frame, basing on the synched time interval. Let us ask ourselves: will the reading of clock A show at the point D the same physical time as we see in the resting frame? To answer without loss of generality, we will still premise that the transformation of time intervals takes place and is determined by (7.35). Then, if the mark B has been put at the point x0 and this point coincided with the clock A at the moment t0 , then the moving observer has to detect the moment of time |
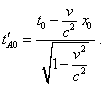 |
(7.36) |
Similarly we can write for the clock’s A coincidence with the point C: |
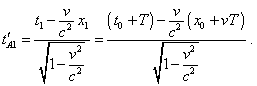 |
(7.37) |
Subtracting (7.36) from (7.37) and making simple transform, yield the value of etalon time interval which the clock A gives in Relativity: |
| (7.38) |
As we can see in (7.38), we yielded a full analogue of (7.35) that corroborates, in the moving frame the clock has to go faster. In our case this already is of no importance. We are interesting in time on the clock A when it coincided with the point D. Using the same technique of calculation, yield |
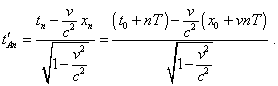 |
(7.39) |
Noting (7.36), we can re-write (7.39) as |
| (7.40) |
Thus, we see that in physical time of resting observer, from the coincidence of clock A with the point B till its coincidence with the point D, n periods of time passed and the clock A shows for this interval of time also n periods of synched time. Since the relative time consists of periods and clocks show us the quantity of periods, the clock’s reading after such single synchronisation of intervals of time will show one and the same relative current time both in the resting and moving frames. Thus, concerning the current time, we have lifted the problem of non-simultaneity of events of which relativists say. After we have synched the time intervals and transmission of momentary value of the current time from one frame to another, the relative physical time in both frames will be synchronous and will count the same number of synched intervals. And even if we take the parts of these intervals, because of linearity of transform, they will be divided in the same degree in both frames. But, – relativists will object, – the values of time intervals in (7.40) are different, and despite same reading of clock at any points of mutually moving frames, the general time will go differently. Yes, from the view of temporarily introduced premise that the time intervals transform, this will be so. But first, speaking not only of some amount of number of periods but of their duration, relativists avoid a direct comparison of clocks but are speaking already of time not limited by the number of periods to which they still reduced their association of time: “we call a clock the system that automatically repeats one and the same process. And the number of repeated processes of such kind – and we can take any process as the first – is just the time measured by clock. The readings of clock simultaneous with some event we call the time of event measured by this clock” [45, p. 416]. This means, there exists the concept of time abstracted from particular measuring instruments and determined as a physical parameter that detects the sequence of events in general meaning of this term. Second and the main is that, when we temporarily took the premise of time transformation, we narrowed the issue to the problem of transformation of time intervals and showed that irrespectively of, whether the intervals transform or not, the current time in the values of synched intervals will go synchronously in the mutually moving frames, and there will be no non-simultaneity of events. |
Contents: / 53 / 54 / 55 / 56 / 57 / 58 / 59 / 60 / 61 / 62 / 63 / 64 / 65 / 66 / 67 / 68 / 69 / 70 / 71 / 72 / 73 / 74 / 75 / 76 / 77 / 78 / 79 / 80 / 81 / 82 / 83 /