V.6 No 1 |
77 |
| The problem of physical time in today physics | |
|
|
V.6 No 1 |
77 |
| The problem of physical time in today physics | |
|
|
7.1.3. The grounds to transform the time in relativistic conception Proceeding from the necessity to give separately the equation of transform for time intervals, it is important to make sure how much grounded is such transform in the relativistic conception. It will be easy, noting that Einstein tried to do so already in his work of 1905. Let us follow the sequence of Einstein’s derivation, to see how he interrelated the paces of time. “If we put |
| (7.14) |
it will be clear that to the point resting
in the frame k, a definite, independent on time set of values x', y,
z will belong. We will first determine Let us make a period in order to understand better, which
parameters relate to which frame. Some time before this citation, Einstein described both
frames so: “Let in the ‘resting’ space we have two
coordinate systems, each with three mutually perpendicular axes that originate from one
point… Let now to the coordinate origin of these systems ( k ), the (constant)
speed v is given in direction of growth of the axis x of another resting
frame ( K ); this speed is passed also to the coordinate axes, as well as to the
corresponding scales and clocks. Then to each moment of time t of the resting
system ( K ), a definite location of the axes of the moving system
corresponds… To each set of values x, y, z, t that fully
determine the place and time of the event in the resting frame, the set of values According to this citation, the set of parameters x,
y, z, t corresponds to the resting frame K and the
set of parameters |
| (7.15) |
However, with it other questions arise. First, if Einstein wrote (7.14), meaning (7.15), he would have to account the transform coefficient of the frame k and to write so as he wrote it further: |
| (7.16) |
As he did not so, he factually says us in this consideration that there are no transforms of spatial parameters along the motion. And if further, basing on the postulate of lightspeed constancy, he comes to the opposite, in this way he again contradicts the statement of problem. Second, it immediately follows from (7.15) that the time “Let from the coordinate origin of
the system k (i.e., from the point
|
| (7.17) |
(which evidences of isotropy of lightspeed in k –
Authors) or, writing out the arguments of function |
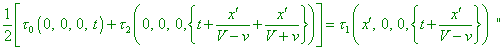 |
(7.18) |
[4, p.14]. Here we have to stop again to analyse (7.18). First, we
see from it that all values of |
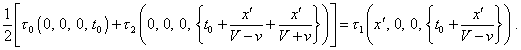 |
(7.19) |
Second, in the second summand of left part and in the right part we see that to the initial moment t0 of the frame K there are added the terms containing x' – the parameter which, as we saw above, relates to another frame k. Is it occasional? Further we will see – no. But anyway the time t0 from the radiation to the moment of reflection t0 , just as the time from the moment of reflection t1 to the moment of reception, cannot be in K determined by x' in the appearance in which it is introduced in the above relationships, and the more to be added to the moment t0 . So we have to correct also (7.18) and to put into it a particular value of x1 which we cannot find more accurately in Relativity because of indefinite degree of time transform ( at this level of Einstein’s proof of his hypothesis). While in classical formalism, just as with (7.14), we can write |
| (7.20) |
The only thing which we could refine in (7.20), given
(7.16), is to add an indefinite transform coefficient for spatial parameters and to
account that according to (7.17), the light is propagated isotropically in the frame k,
and the value |
| (7.21) |
With these refinements, the appearance of summands in the
above terms with time of (7.18) will naturally change. To see this change, we have to
account that the path from radiator to the mirror, from the point of K (due to
motion of the reflection point |
| (7.22) |
and the path from the mirror to the receiver from the point of frame K is |
| (7.23) |
Given (7.22) and (7.23) and the postulate of lightspeed constancy in all frames declared by Einstein, (7.19) will take an appearance |
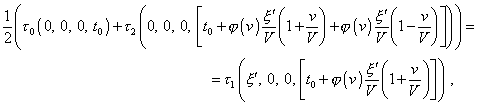 |
(7.24) |
or otherwise |
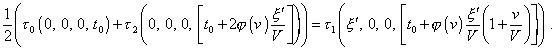 |
(7.25) |
In this expression we immediately see that “If we take x' infinitesimal, it follows from this (from (7.18) – Authors) that |
| (7.26) |
or |
| (7.27) |
[4, p. 14]. We see from (7.26) and (7.27) that all ‘slips of the pen’ that we corrected in the course of Einstein’s derivation appeared in fact quite realised substitutions. We see in his formulas how the derivatives in time t appeared which, as we saw above, is not a variable but only determines the moment of beam radiation in K. Now the derivative in x' appeared also, though this parameter was constant, too, and it did not become variable because it was taken small, while Einstein will integrate over it. This parameter only determines the location of reflection point in the frame k, nothing else. Thus, we can ascertain that Einstein’s attempt to substantiate the necessity of time contraction through comparing the time intervals in mutually moving frames reduced to juggling with formulas and symbols. In reality, the very fact of time contraction, and of anisotropic time transform that follows from Lorentz transforms, is absurd. Even if we consider time as relative time that means the correlation of sequence of events with some specific periodic process, it is enough to take as an example a simple pendulum to make sure how senseless are such transformations. Actually, let us take a plane pendulum and try to check the processes in the moving frame. According to the relativistic formalism, dependently on the orientation of plane of swing relative to the frame’s motion, its mass, elasticity of springs and radius of swing have to vary, and the variations have to be detectable straight in the moving frame. At the same time, we can detect the events at some chosen point equally at most different orientations of periodic process, as for us the matter of importance is, at a point where we observe the event, the body – carrier of periodic process to coincide with the studied body (to meet it). Around this point the plane of pendulum can take an arbitrary position in space. And always the pendulum will come to the point of meeting with the studied body. And, as we always can juxtapose to any specific point where the event occurred many differently oriented pendulums, the choice of true coefficient of time transform becomes indefinite and, hence, insolvable. This is why Einstein’s derivation basically could not give a result. And Einstein understood, he cannot prove the time transformation, basing on particular model of intervals transmission. So in other his work, “The principle of relativity and its corollaries in today physics” [17], he gives another proof of interrelation of times. Here he already does not try to direct a beam but simply writes: “We have put forward the task to find the relationships that interrelate these two sets of coordinates. Using the homogeneity of time (?! – Authors) and space, we can show that these relationships have to be linear, i.e. t and t' are interrelated as |
| (7.28) |
…, coordinates x, y, z, x', y', z' are interrelated as |
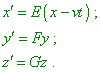 |
(7.29) |
To find the constants A, B, C, D, E, F, G in (7.28) and (7.29), note that according to the principle of lightspeed constancy, the speed of propagation has one and the same value c relative to both frames, i.e., equations |
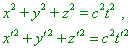 |
(7.30) |
are equivalent. Substituting in the second equation t', x', y', z' by their values from (7.28) and (7.29) and comparing with the first equation, yield the transform formulas…” [17, p. 152–153]. We see from this citation that Einstein simply substituted the derivation of transform formula for temps of time by the proof that the 4-interval based on postulate, not on the experimentally checked fact, is invariant for the Lorentz transforms. But when comparing the pace of time, we factually compare the times at different points of inclined plane of events; this discrepancy remains and, as we already said, it cannot be solved by the methods with which relativists try to solve it. |
Contents: / 53 / 54 / 55 / 56 / 57 / 58 / 59 / 60 / 61 / 62 / 63 / 64 / 65 / 66 / 67 / 68 / 69 / 70 / 71 / 72 / 73 / 74 / 75 / 76 / 77 / 78 / 79 / 80 / 81 / 82 / 83 /