SELF |
58 |
S.B. Karavashkin and O.N. Karavashkina |
|
|
|
SELF |
58 |
S.B. Karavashkin and O.N. Karavashkina |
|
|
|
4. The pattern of light propagation in the moving inertial reference frame from the point of relativistic mechanics Above we showed: when ignored the difference in description of material points and field processes, this was the cause because of which relativists formulated the incorrect postulates of their conception. Basically, this lifts the necessity to continue the analysis of relativistic conception. None the less, in this section we will specially consider the distinctions of field processes description in passing between the inertial frames from the point of Lorentz transforms, in order to lift the speculation as if incorrect premises are able to bring us the physically associative results. As the initial equations of equiphase surfaces excited by the source resting in the resting frame, we have all grounds to take the system (3.1) which we used above to find classically the direct coordinate transformation. Instead (3.2) used before, we have to write the trivial Lorentz transforms which will determine the passing between the inertial frames in the relativistic conception: |
 |
(4.1) |
After manipulation, yield for the moving frame |
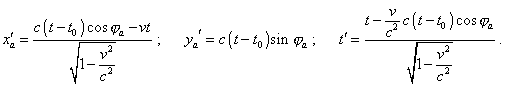 |
(4.2) |
The dynamic diagram plotted with (4.2) is shown in Fig. 4.1.
|
Fig. 4.1. Dynamic diagram of propagation of equiphase surfaces of light in the moving frame from the point of relativistic conception; the frame moves with the speed v = 0,8 c with the positive values of the axis x of the resting frame
|
The diagram shows that with the Lorentz transforms, just as with the direct classical transform, the equiphase surfaces do not transform, but the plane of events inclines with respect to the moving coordinate system. To understand the consequences of such inclination, consider a 2-D pattern, how the equiphase surfaces propagate in the plane (x', ct' ) passing the world line of the source of light of Fig. 4.1. This projection is shown in Fig. 4.2.
|
Fig. 4.2. Dynamic diagram of propagation of equiphase surfaces of light in the plane (x', ct' ) of the frame from the point of relativistic conception; the frame moves with the speed v = 0,8 c with the positive values of the axis x of the resting frame; the red markers show the projections of equiphase surfaces onto the plane; the world line of the source is denoted in green; the blue line is the world line of the observer resting with respect to the dotted frame
|
To make the diagram visual, we added the world line of the
observer (blue line) and drew the projection of the plane of events of this observer (the
green-blue line drawn in parallel to the axis x' ), to draw the Reader’s
attention that the solutions yielded with the Lorentz transforms are inconsistent with the
statement of problem on whose basis Einstein yielded these formulas. Actually, according
to the statement of problem, the physical time was involved in both frames, which means
synchronisation of all identical clocks in each frame: “Let
through the resting clocks in the resting frame and with the help of light signals, in the
way shown in section 1 we determine the time t of the resting frame for all
points of this last in which the clocks are located. Let then the time From this, the clocks of all observers in the moving frame have to read the synchronised time. But when we apply this stipulation to the dynamic diagram in Fig. 4.2, it appears that all observers located on one plane of events with the selected observer will not see at all the source and equiphase surfaces, as all material objects, light waves, sources and observers will be located on the inclined plane (in this case on its projection (x', ct' ) ). Therefore, nothing can be located out of this plane at any chosen moment of time, i.e. namely in the regions through which the plane of events goes (the green-blue line) of the selected observer in Fig. 4.2. True, we can premise that the diagram in Fig. 4.2 describes not the signal propagation in the physical time but is only some regularity characterising the signal propagation in the moving frame yielded in the transforms. If we look the whole diagram, the observers at each point, at some moment of time (out of the plane of events) will, nevertheless, see these equiphase surfaces. But then the Lorentz transforms will give us not final but intermediate solution which we yet have to agree additionally with the statement of problem. To put the solution into agreement with the statement of problem, we have to recalculate the inclined plane of events produced in the Lorentz transform to the physical time introduced by Einstein after the statement of problem in this frame. This pass was necessary also because we do all these measurements in our moving frame which is at rest for us and generally moves for the observers in other frames. This means, as in our frame we use the physical time, the true properties of the Lorentz transforms we can reveal only passing to the dotted (in this case) frame. To do so, let us do this transform from the solution (4.2)
to the solution describing the propagation of equiphase surfaces in the units of physical
time in the moving frame. For it, we have to transform x'a(t,
t'0, To pass in these regularities from the time parameter t0 characterising the moment when the equiphase surface was radiated from the point of resting frame to its equivalent t'0 in the moving frame, pay attention that the stipulation t = t0 has to correspond to the stipulation t' = t'0 . Hence, from the last equation of the system (4.2) we yield |
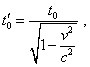 |
(4.3) |
or |
| (4.4) |
The regularity (4.4) shows that the equal time intervals of the light radiation by the source in the resting frame will correspond to the equal time intervals in the moving frame. As we will show below, in the relativistic conception we may not conclude from it concerning the period of signals detected by the observer, as in this case we have to use the complete expression to transform the times in (4.2). And (4.4) is true only for the relation between the moments of radiation of the light equiphase surfaces. But these values keep proportion, and this makes the problem much easier. Then, we may substitute (4.4) to the same equation describing the time transform in (4.2) and yield the relation between the physical time of resting and moving frames: |
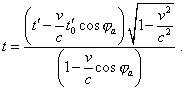 |
(4.5) |
Basing on (4.4) and (4.5), we can find the relation between the time intervals of equiphase surfaces propagation from the moment of their radiation to the current time in the related frames: |
 |
(4.6) |
We see from (4.6) that on one hand, for each given
direction |
| (4.7) |
yield |
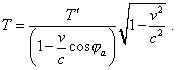 |
(4.8) |
At the same time, if we take two sequential moments of time t01 , t02 and t'01 , t'02 at which the equiphase surfaces were radiated, with (4.4) we will yield |
| (4.9) |
We see from (4.8) and (4.9) that the right parts of these
equations are equal only if cos To finish the first stage of this passing to the dotted coordinates, we, substituting (4.4), (4.6) and (4.6) to the first two equations of the modelling system (4.2), yield the sought regularities of coordinates of equiphase surface against the time parameters of the moving frame: |
 |
(4.10) |
Thus, by way of additional transforms, we yielded some system of equations (4.10) which without mediation of space-time parameters of the frame S describes the equiphase surfaces in the frame S' . We can notice, these equations satisfy the light speed constancy. It is easy to check it, finding the derivatives of both equations (4.10) with respect to t' : |
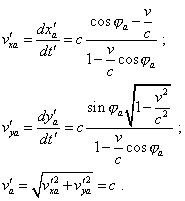 |
(4.11) |
We also have to notice that expressions (4.10) satisfy the equation |
| (4.12) |
that is equivalent to the Einsteinian 4-D interval. We can easily check it, too, given in accordance with (4.11) |
| (4.13) |
and we can represent the expression for x'a in (4.10) as |
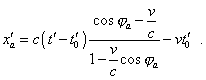 |
(4.14) |
Contents: / 53 / 54 / 55 / 56 / 57 / 58 / 59 / 60 / 61 / 62 / 63 / 64 / 65 / 66 / 67 / 68 / 69 / 70 / 71 / 72 / 73 / 74 / 75 / 76 / 77 / 78 / 79 / 80 / 81 / 82 / 83 /