V.6 No 1 |
67 |
| The problem of physical time in today physics | |
|
|
V.6 No 1 |
67 |
| The problem of physical time in today physics | |
|
|
6.3. Mach’s absolutisation of relative orbital motion Having sorted out Einsteinian treatment of Mach’s principle of relativity, consider this issue in the original statement of Mach which he stated in his “Mechanics”. In brief, he stated it so: “I think existent only relative motion… and I cannot assume here any difference between the orbital and forward motion. If the body revolved relative to the sky of resting stars, the centrifugal forces arise, and if it revolved relative to another body, not relatively the sky of resting stars, centrifugal forces are absent. I am not against to call the first motion absolute, only if we do not forget that it means nothing else than revolving relative to the sky of resting stars. Can we, holding the Newtonian vessel with water being at rest, revolve the sky with stars relative to it and prove the absence of centrifugal forces in this case?” [61, p. 60].So Mach raised the issue of relative orbiting motion which is well deeper than relativists interpreted it. So deep that it made many adherents of classical mechanics even to deny partially the Newtonian principles in some models containing the orbiting: “the acceleration of material point relative to a non-inertial reference frame arises under affection of the force F from a definite body (or bodies), as well as resulting from the accelerated motion of the frame S' relative to the inertial frame S. We can treat the acceleration of material point relative to the non-inertial reference frame as the result of inertial forces. We cannot point for these forces the source as a definite body affecting this material point. So this force of inertia has not a related counteracting force, in other words, the forces of inertia, as opposite to the forces of interaction, do not obey the third Newton law” [62, p. 166]. With it all, if we approach the issue of relative orbiting raised by Mach with all thoroughness which the classical formalism allows, we will reveal that Newton was right stating so: “The effects which distinguish absolute from relative motion are the forces of receding from the axis of circular motion. For there are no such forces in a circular motion purely relative, but in a true and absolute circular motion, they are greater or less, according to the quantity of the motion” [2, p. 34]. To prove Newton’s conclusion, let us understand more precisely, what namely he meant separating the orbiting into the absolute and relative. Giving an example of the vessel with water, Newton explained it as follows: “If a vessel, hung by a long cord, is so often turned about that the cord is strongly twisted, then filled with water, and held at rest together with the water; after, by the sudden action of another force, it is whirled about the contrary way, and while the cord is untwisting itself, the vessel continues, for some time in this motion; the surface of the water will at first be plain, as before the vessel began to move ” [2, p. 34]. In other words, while the walls of vessel involve the water into orbiting due to the liquid friction, and so all its parts remain resting relative to the inertial frame in which we are experimenting, the motion of pail with respect to water is relative, as only pail moves, not the water in it. And the water not necessarily has to be just in the vessel. The same relative orbiting would take place if the water was in the vessel that stands near the orbiting vessel, or would be put into the vessel that is put into another vessel that orbits and has no constraint with this first. Naturally, the forces of inertia do not arise in the liquid with it, as the liquid rests, but in the orbiting vessel these forces exist, and if the orbiting is too fast, the vessel can destroy, which would evidence the presence of these forces of inertia affecting the vessel, not the liquid in it. Here we also find the disproof of Mach’s premise that
the inertia forces can be substituted by the attraction of stars which he formulated in
the following way: “instead
to interrelate the moving body K to the space (to some coordinate system), let us
consider its immediate relation to the bodies of the world through which we only
can determine the coordinate system … Instead saying, the distance and speed
of mass in space remain constant, we can use the expression that the average acceleration
of the mass |
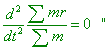 |
(6.17) |
[61, p. 57]. We would like to draw the Reader’s attention, how Mach appeals to the resting stars and even in the expression (6.17) expresses them as static masses. Achievements of astronomy at his times gave him no grounds to say so, as at that time it was already discovered that the stars and their clusters move in space, are accelerated, participate in orbiting relative to their axes. This all has no effect on the vessel with water on the Earth, until we did not twist it, or anyway, to say precisely, this effect is negligibly small comparing the revelations of centrifugal forces. And even if this effect were considerable, irrespectively of orbiting of water in the vessel, it would tend to the walls of vessel, as both during the orbiting and out of it, it is at some distance from the axis of orbiting. True, with it we would have to prove additionally that the mass centre of the universe is just on the axis of vessel, as Mach in (6.17) showed namely second derivative of the expression for the centre of masses. And it is an insoluble problem to prove the presence of the mass centre on the axis of vessel’s orbiting in this particular experiment, noting the multitude of such revolutions occurring at the same time not only on the Earth but in the universe. But the fact that galaxies can orbit, doing not exciting the centrifugal forces of inertia in the resting vessel on the Earth just speaks of incorrect Mach’s reference to the universal nature of centrifugal forces. Here we come to the Newtonian definition of absolute orbiting that reveals the centrifugal forces of inertia. Newton has formulated it so: “but the vessel, by gradually communicating its motion to the water, will make it begin sensibly to evolve, and recede by little and little from the middle, and ascend to the sides of the vessel, forming itself into a concave figure (as I have experienced), and the swifter the motion becomes, the higher will the water rise, till at last, performing its revolutions in the same times with the vessel, it becomes relatively at rest in it. This ascent of the water shows its endeavour to recede from the axis of its motion; and the true and absolute circular motion of the water, which is here directly contrary to the relative, discovers itself, and may be measured by this endeavour. At first, when the relative motion of the water in the vessel was greatest, it produced no endeavour to recede from the axis; the water showed no tendency to the circumference, nor any ascent towards the sides of the vessel, but remained of a plain surface, and therefore its true circular motion had not yet begun. But afterwards, when the relative motion of the water had decreased, the ascent thereof towards the sides of the vessel proved its endeavour to recede from the axis; and this endeavour showed the real circular motion of the water perpetually increasing, till it had acquired its greatest quantity, when the water rested relatively in the vessel. And therefore this endeavour does not depend upon any translation of the water in respect of the ambient bodies, nor can true circular motion be defined by such translation. There is only one real circular motion of any one revolving body, corresponding to only one power of endeavouring to recede from its axis of motion, as its proper and adequate effect; but relative motions, in one and the same body, are innumerable, according to the various relations it bears to external bodies, and like other relations, are altogether destitute of any real effect, any otherwise than they may partake of that one only true motion. And therefore in their system who suppose that our heavens, revolving below the sphere of the fixed stars, carry the planets along with them; the several parts of those heavens and the planets, which are indeed relatively at rest in their heavens, do yet really move. For they change their position one to another (which never happens to bodies truly at rest), and being carried together with their heavens, partake of their motions, and as parts of revolving wholes, endeavour to recede from the axis of their motions” [2, p. 34]. In other words, revolution is absolute if the body takes a part in it, as only in this case the body is affected by the force that changes the direction of its motion and makes it moving in the circle or ellipse or hyperbola. If other bodies, not the studied body participate in this motion, the forces curving the trajectory do not affect this body; hence, the inertial forces to not reveal themselves in the body. Mach has neglected in his premises a simple and obvious fact that resting stars just prove his statements incorrect, as, should their own revolutionary motion affected the water in the vessel in the proportion in which the centrifugal forces do, the water in the resting vessel would take the corresponding shape, being in the same process of relative motion with the remote stars. Things go otherwise; hence, Newton is right saying that inertia is the consequence of the changing pattern of body’s motion, not of the motion of surrounding bodies. But, – the adherents of Mach’s conception will object, – “if the body revolved relative to the sky of resting stars, the centrifugal forces arise, and if it revolved relative to another body, not to the sky of resting stars, there are no centrifugal forces” [61, p. 60]. If speaking of relative and absolute revolution and features of their revelations, we already have answered this question and showed, though kinematically the body participating in the relative motion also has an acceleration relative to the body that participates in the absolute revolution, none the less, as Newton concluded, the difference is determined by presence of affecting force deflecting the body from the direct trajectory. And due to this affection, the forces of inertia just reveal themselves in the absolute revolution. We also have answered another part of question, showing illegal to call the centrifugal forces – the forces of body’s interaction with the fields of surrounding stars and in this way corroborating Newton’s conclusion that the origin of inertia forces is connected directly with the body affected by the force. But we still have unanswered the question, why in some cases we immediately feel the forces of inertia and in some other – do not, if in each affection of the external force, the force of inertia reveals itself? |
Contents: / 53 / 54 / 55 / 56 / 57 / 58 / 59 / 60 / 61 / 62 / 63 / 64 / 65 / 66 / 67 / 68 / 69 / 70 / 71 / 72 / 73 / 74 / 75 / 76 / 77 / 78 / 79 / 80 / 81 / 82 / 83 /