SELF |
56 |
S.B. Karavashkin and O.N. Karavashkina |
|
|
|
SELF |
56 |
S.B. Karavashkin and O.N. Karavashkina |
|
|
|
With the said, let us use the second approach to determine the pattern of equiphase surfaces in the moving frame and plot the equiphase surfaces in premise that the observer’s frame rests but the source moves along the negative x with the same speed v. Outwardly this problem seems to be fully same as the previous and even more senseless from the view of principle of equivalence of the inertial frames on which relativists based their conception. None the less, let us model the process for this case. First of all, just as in the previous model, premise that
at the initial moment of our study the origins of resting and moving frames coincide. As
in this representation the frame rests while the source moves with some speed vs , then supposing that at the moment t' = 0 the source was in the
coordinate origin, we can write the equation of some arbitrary equiphase surface for t
|
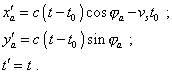 |
(3.8) |
Comparing (3.8) with (3.3), we see the difference in modelling systems of equations. In the right part of the first equation of (3.8) we see the product of the source speed at the moment when it radiated the studied equiphase surface vst0 , while in (3.3) there was the product of the frame’s speed (equal, in this case, to the speed of source) into the current time vt since we started the observation as the whole. Although outwardly it seems insignificant, this difference would be basically impossible if these two approaches were fully equivalent. And this outwardly little change appears to have a significant effect on the pattern of equiphase surfaces whose shape we see in the dynamic diagram in Fig. 3.2.
|
Fig. 3.2. Dynamic diagram of propagation of the light equiphase surfaces when the source moves with the speed vs = 0,8 c along the negative values of axis x, for the moments of time from t0 = 0 to t0 = 6T , where t0 is the moment of the equiphase surface radiation; the world line of the observer is denoted in blue
|
In this diagram we see the typical transformations of the equiphase surfaces with the unchanged plane of events. Seemingly, we yielded what expected from the first model – from direct passing between the inertial frames; none the less, this is already irrelevant to the above solution; so it doubts the statement on which there formed the postulatory basis of Relativity: “of all thinkable spaces R1 , R2 etc. moving anyway in relation to each other no one can gain the preference” [21, p. 456]. Despite the difference, with such approach the observer will detect the frequency transformation also. To show this, use (3.8). If the source radiated the equiphase surface at the moment t0 and observer detected it at t1 , then, according to (3.8), the detection time in case of longitudinal Doppler-effect will be determined as follows: |
| (3.9) |
Let the next equiphase surface to be radiated at t0 + T and detected at t1 + T ' . Then the moment of detection of this equiphase surface will be determined as |
| (3.10) |
Subtracting (3.9) from (3.10) and doing a simple transformation, yield |
| (3.11) |
where plus denotes the motion from the observer and minus – motion to the observer. |
On the whole, for small speeds of frame in one case and of source in another, (3.6) and (3.11) give same result in the first approximation, as it follows from (3.6) that at small speed |
| (3.12) |
But at speeds comparable with the speed of light, such approximation will not be true, and regularities for the Doppler effect will be different. It is well seen in Fig. 3.3 plotted on the basis of (3.6) and (3.11) relatively.
|
Fig. 3.3. Relative variation of the period of signal against the speed of frame (the curve I) and speed of source (the curve II); the regularity I was plotted with (3.6), and the curve II – with (3.11) |
Contents: / 53 / 54 / 55 / 56 / 57 / 58 / 59 / 60 / 61 / 62 / 63 / 64 / 65 / 66 / 67 / 68 / 69 / 70 / 71 / 72 / 73 / 74 / 75 / 76 / 77 / 78 / 79 / 80 / 81 / 82 / 83 /