SELF |
66 |
S.B. Karavashkin and O.N. Karavashkina |
|
|
|
SELF |
66 |
S.B. Karavashkin and O.N. Karavashkina |
|
|
|
6.2. Correctness of Einstein's equivalence of centrifugal forces to the gravity attraction of stars With the Poincare rule, consider the problem of
equivalence of centrifugal forces to the gravity attraction of the surrounding stars in
Einstein’s interpretation. For it, draw a simple model. Some body with the mass mm orbits with the angular speed
|
Fig. 6.1. The scheme to calculate the affection of external gravitating masses onto the appearance of centrifugal force in relativistic representation
|
According to the Einsteinian statement of problem, assume the distribution of surrounding masses such that the total affection of these masses onto the central body me , as well as onto the body mm , if we put it into the centre, is zero, which provides the absence of non-compensated force affecting the centre of orbiting. Given the static state of surrounding masses (after Mach), we can, using the Newton gravity law, write this condition so: |
| (6.1) |
where Now we have to write the similar equality for the total force affecting the orbiting body when it is located at the distance rm from the axis of orbiting. This equality will have quite expectable appearance |
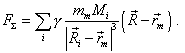 |
(6.2) |
Noting that the masses are remote, we can write (6.2) approximately as follows: |
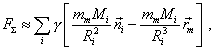 |
(6.3) |
and as far as the first summand of the right part in accordance with (6.1) is zero, we will finally yield with enough accuracy |
| (6.4) |
Outwardly it can seem that when writing (6.4), we corroborated Einstein’s and Mach’s derivation that centrifugal force can be presented as a non-compensated affection of surrounding gravity masses. The only nuance is that the dependence of the body on orbiting frequency is absent in (6.4). It means that the force which relativists think to be equivalent to that centrifugal will remain its value, and the main, the direction, irrespectively of, whether the body is orbiting or resting relatively the central body. With it, even in the non-relativistic case, we see the change of spatial orientation of centrifugal forces in time and dependence of their amplitude on the angular speed of orbiting body. It follows from this that, introducing such interpretation of centrifugal force, relativists, in accordance with (6.4), have to introduce an additional dependence of the orbital frequency either on the change of distance to the gravitating masses or on the masses themselves, as the length of constraint rm and the body’s mass mm remain unchanged, and this increase has to go in proportion inverse to rm /Ri3 . Given also that here on the Earth we each second have multitude of such orbitings with different frequencies and radii (and how many in the whole universe!), such change of radii and gravitating masses, and in such proportion as experimenter wishes, is basically impossible. To complete the analysis of relativistic understanding, we have to consider one more possibility of Einsteinian substantiation of equivalence of centrifugal force with the orbiting of remote gravitating masses which George Telezhko, our colleague from the Astroforum, pointed in the discussion [57] of the first version of this work. His idea was in trying to account the vectorial gravity potential of surrounding masses that arises in their motion about the pail (or the pail about the masses, which, from the relativistic view, is same). More exactly, it was formulated so. “Until these fields are static, only scalar potential is present. But if the source of field moved, it delivers to the resting observer a new inconvenience in the form of vectorial potential of the following kind: |
| (6.5) |
– in the first approximation (where Agi is the vectorial gravity potential, The y-component of the potential (we will normalise the gravity constant to 1) is” [57, post 10] |
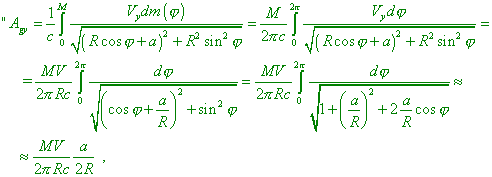 |
(6.6) |
at – Einsteinian E = mc2 of the trial body (i.e., the total energy of the body is its potential energy in the potential of the universe); – inertia (the acceleration in such potential produces the ‘gravi-Lorentz’ force affecting against the acceleration and proportional to the acceleration); – all relativistic effects (re-calculation of potential by any observer into the potential in which the vectorial part is absent makes necessary to transform the physical values after Lorentz)” [57, post 6]. And though the very idea to account the vectorial potential arising due to the motion of source cannot be a direct argument on which Einstein could base but is rather an attempt of Mr Telezhko to substantiate Mach’s and Einstein’s hypotheses proceeding from the further development of theoretical physics, none the less, it is interesting to analyse this premise to generalise the above derivation. To complete the consideration, we first have to account that according to the above study substantiating the conditions of electromagnetic field [58], in this problem two cases are basically different: the body’s motion in the field of resting source and the motion of source relative to the resting body. This difference is caused by the finiteness of speed with which the excitation propagates in space. So we will some extend Telezhko’s model, assuming both cases possible – when the sphere of remote stars moves relatively the body and when the body moves relatively this sphere which we model through the cylindrical ring cut off the sphere. If the body moved in the field of resting source (in this model – massive ring), it interacts with the static field of this source. With it, the force arises only due to the inhomogeneity of the source field (unambiguously, in presence of this inhomogeneity), and it arises just at the moment when the body comes to a particular area of the field, since the very field, as we already said, is static and present at the point before the studied body appeared there and irrespectively of, whether the body is at this point. It is clear that in spherical arrangement of gravitating masses, the potential inside the sphere will be constant, as “the resulting gravity force produced by the spherical layer as the whole has to be identically zero for any point A laying inside the sphere of radius R. Therefore, the force of attraction affecting the body travelling inside the Earth (in the considered model – inside the massive shell – Authors) will be equal to the gravity force produced by the layer of radius equal to the distance from the body to the centre of Earth” [59, p. 183–184]. And, as in this version of our problem a considerable gravitating mass is absent between the centre of orbiting and the orbiting body and the potential of outer gravitating masses is constant in time, the vector gravity potential also will be zero, irrespectively of the pattern of body’s motion. And the vectorial potential will vanish, despite the expression (6.5) on which Mr Telezhko bases his derivation as if is not zero. To understand, why the vectorial potential vanishes in case of static field irrespectively of (6.5), we have to account the nature of vectorial potential. The gravitational vectorial potential was introduced (by Mr Telezhko in that number) by an analogy with the vectorial potential of electromagnetic field, on the basis of common regularities of the theory of potential. So this potential, just as in the theory of electromagnetic field in the region out of gravitating (in this analogy) masses has to satisfy the known relationship [53, p. 84]: |
| (6.7) |
where |
| (6.8) |
Besides, the vectorial potential is known to be determined by the expression [53, p. 87] |
| (6.9) |
where, in this case, It immediately follows from (6.8) that in case of resting sphere the vectorial gravity potential Ag is stationary and independent of time. And it follows from (6.9) that the density of flux j(R,
But if the source moved, the excitation caused by the sphere’s motion will affect the body with a time delay necessary the excitation to reach the point where the body is located. In this connection, two versions of consideration are possible. In the first version, the sphere starts and finishes its motion together with the start and finish of the motion of orbiting body. In this case, the delay is the matter of principle, as both in Mach’s, Einstein’s and Telezhko’s models the gravitating masses are far away from the Newtonian orbiting pail; so, if the cylindrical ring rotated, it raises great questions not only to the conditions and forces able to make this ring moving synchronously with the start of body’s motion but also to the arising of centrifugal force without time delay comparing the start of pail’s motion, which we do not find experimentally in case of centrifugal forces. At the same time, noting the astronomic size of gravitating ring, the delay can be so considerable that the constraint between the body and fulcrum at definite conditions can be destroyed before the excitation from the ring remote by millions of light years will reach the body. We can yield one more solution from Mr Telezhko’s model, supposing that the narrow cylindric ring rotates stationary, and the centrifugal force arises in the body’s motion relative to the ring. In this case, basing on general expression (6.5), the start of ring’s motion at the moment when the body starts its orbiting relative to stars is not a requirement, and the conclusion (6.6) by Mr Telezhko is applicable – true, with the reservation that in this expression we will think under the speed not the speed of body but the stationary speed of gravitating ring. Or rather, we can use even not (6.6) but initial (6.5), as the case of inner region of the ring does not need so complicated integration, and the result will be other than in (6.6). Given the constant scalar potential inside the ring, with the speed of stellar ring v0 , (6.5) will take the form |
| (6.10) |
where In (6.10) both scalar potential and speed of ring are constant. Therefore, the tangential component of vectorial gravity potential Agr is constant in the whole inner region of ring and its distinction from the scalar potential is that it is a vectorial value directed in this case perpendicularly to the radius of ring. Evolving the analogy with electromagnetism on whose basis Mr Telezhko has introduced the concept of vectorial gravity potential, we can conclude that the potential force caused by the vectorial potential will be zero. Actually, noting Agr is constant, |
| (6.11) |
While the circulation of vector |
| (6.12) |
just as Mr Telezhko expected, does not vanish. But this non-zero value is limited by the case when the orbital plane of revolving body contains inside itself the rotation axis of the massive ring (see Fig. 6.2). |
Fig. 6.2. The orbiting of a body in case when its axis of orbiting coincides with the rotation axis of the massive ring
|
In the particular case, when axes of the body and the ring coincide, |
| (6.13) |
With (6.13) we can determine the average strength of the magneto-gravitation field inside the region covered by the loop L as |
| (6.14) |
and finally, by an analogy with the Lorentz force, |
| (6.15) |
where V is the speed of the body’s orbiting and m is the mass of body. This calculation is estimating, of course, and in passing from the ring to the sphere, the expression (6.15) will become much more complicated, due to the unequal rotation speeds of selected rings; none the less, the main feature which the solution shows will remain. This feature is, the direction of magneto-gravitating force depends on the direction of body’s orbiting. When the direction is changed to the opposite, the direction of force also changes. Hence, should the centrifugal force were caused by the vectorial potential, with the changed direction of orbiting we would not see the body tending to fly away from the fulcrum, irrespectively of the direction of orbiting, as Newton pointed. With one direction of orbiting, the body would tend to fly away from the fulcrum, and when it changes the direction of orbiting to the opposite, it would fly closer to the fulcrum – which disagrees with the practice. And when the body’s orbit is perpendicular to the plane of gravitating ring, then, according to (6.15), the centrifugal force would be directed not from the centre, as it is done for the centrifugal force, but perpendicularly to the plane of body’s orbit, slewing it into the plane of ring, – which we also do not see in the practical study of centrifugal forces, but it is so in the practice of loops interacting with the current. In mechanics, on the contrary, we observe the gyroscopic effect conserving the orientation of the axis of revolution in space. The second variant of the body’s orbiting in the field of vectorial gravity potential, when the axis of ring’s rotation is out of plane of body’s orbiting (see Fig. 6.3), brings us to the zero value of circulation due to the constant value and direction of vectorial potential in the whole limited region of the body’s orbiting. |
Fig. 6.3. The scheme of body’s orbiting in case when the rotation axis of the massive ring is out of the plane of body’s orbiting
|
Even if we proceed from the non-uniform distribution of gravitating masses in the universe which could cause some redistribution of the vectorial potential in space, its main feature would reveal itself both in coincidence and non-coincidence of the axes of revolution of the gravitating ring and orbiting body. Namely, with a definite direction of revolution, the force would be directed outwards, and with the change of direction, the direction of centrifugal force would change, too. And with the perpendicular direction of orbiting, the force would be directed outwards, and with the change of direction of orbiting the change of centrifugal force would also change. Thus, having analysed the main variants of possible affection of the vectorial gravity potential onto the orbiting body, we come to conclusion that it is impossible to identify with the centrifugal force – the power affection caused by the vectorial potential. From this consideration, there follows not an incorrectness of classical formalism which connects the centrifugal force of inertia with the very body, of which Einstein said so: “If the Newtonian laws of mechanics and gravity do not admit such interpretation, we can rather think it to be the demerit of these theories”, – but an incorrectness to substitute the internal inertial properties of the body by some external affection. Factually, noting that the centrifugal force, according to all experimental data and many centuries of experience, changes not due to change of location of the celestial bodies but exceptionally due to our wish to change the speed of orbiting of the studied body and a strong dependence of centrifugal force just on the angular speed, – we have to admit, this force, in full accordance with Newtonian theory, actually follows from the inertial property of a material body and is determined by the conditions changing the state of its motion due to the curved trajectory which this body encounters orbiting about the centre. According to Newton, “DEFINITION III. The vis insita, or innate force of matter, is a power of resisting, by which every body, as much as in it lies, endeavours to persevere in its present state, whether it be of rest, or of moving uniformly forward in a right line. This force is ever proportional to the body whose force it is; and differs nothing from the inactivity of the mass, but in our manner of conceiving it. A body, from the inactivity of matter, is not without difficulty put out of its state of rest or motion. Upon which account, this vis insita, may, by a most significant name, be called vis inertia, or force of inactivity. But a body exerts this force only, when another force, impressed upon it, endeavours to change its condition; and the exercise of this force may be considered both as resistance and impulse; it is resistance, in so far as the body, for maintaining its present state, withstands the force impressed; it is impulse, in so far as the body, by not easily giving way to the impressed force of another, endeavours to change the state of that other” [2, p. 25]. As we can see from the citation, this rule concerns not only the acceleration and deceleration of the body but it also changes the direction of its motion. The body to change the direction of its motion without change of the speed, we have to affect it by a force perpendicular to the motion. And affecting the body by some force, we inevitably rise the body’s resistance to this acceleration, due to which, basically, the centrifugal force arises.
|
Fig. 6.4. Th experiment with the Zhukovsky stool
|
An additional corroboration, how much absurd is to
substitute the centrifugal force by the gravity affection of remote masses, is the known
experiment with the Zhukovsky stool. “Consider one more experiment, with the Zhukovsky stool. A man stands
on the resting Zhukovsky stool and holds in arms an axis of a massive wheel, so that it
continues the rotation axis of the stool (Fig. 6.4). initially the wheel does not rotate,
then a man drives it up to the angular speed |
| (6.16) |
where J1 is the moment of inertia of the wheel and J2 is the moment of inertia of the man and stool” [60, p. 80]. This simple experiment shows that we have to seek the nature of all forces of inertia arising in the orbiting exceptionally in the system itself, not in the interaction with remote objects, which makes basically incorrect the relativistic approach to the equivalence of inertial and non-inertial reference frames. |
Contents: / 53 / 54 / 55 / 56 / 57 / 58 / 59 / 60 / 61 / 62 / 63 / 64 / 65 / 66 / 67 / 68 / 69 / 70 / 71 / 72 / 73 / 74 / 75 / 76 / 77 / 78 / 79 / 80 / 81 / 82 / 83 /