SELF |
60 |
S.B. Karavashkin and O.N. Karavashkina |
|
|
|
SELF |
60 |
S.B. Karavashkin and O.N. Karavashkina |
|
|
|
At the same time, as we saw in the section 3, the classical theory transforms the field processes basically otherwise. In presence of luminiferous medium, in classical conception which accounts the features of light wave propagation in this medium, there exist four, not two patterns of dynamic field processes: – the pattern produced by the source resting with respect to the luminiferous medium; in this pattern the asymmetry of equiphase lines is absent and it is described by the system (3.1), let us call it the pattern F; – the map of the pattern F which the observer moving with respect to the luminiferous medium sees. The asymmetry of equiphase surfaces is absent in this pattern, too, but all surfaces as the whole are shifted in time with the shift of frame with respect to the luminiferous medium. This pattern is described by the system (3.3); let us call it the pattern F’; – the pattern of equiphase surfaces produced by the source moving with respect to the luminiferous medium from the point of observer resting with respect to this medium. This pattern has an asymmetry of equiphase surfaces which is dependent on the speed of source with respect to medium. This pattern is described by the system (3.15), let us call it the pattern G; – finally, the fourth pattern describes the map of pattern G at the observer moving with respect to the luminiferous medium. This pattern, just as the pattern G, contains the asymmetry of equiphase surfaces that depends not on the observer’s speed but only on the speed of source with respect to the medium. This pattern differs from G, as the speed of the spatial shift of the pattern of equiphase surfaces as the whole change in time. Let us call it the pattern G’. Although the classical conception describes four patterns
of processes and they all are independent from each other, we may not pass from any to any
of them. The physical properties of luminiferous substance much limit the possible
transforms of the field patterns. In particular, we may not do the transition F We can show these features systematically as the graph of admissible transforms, see Fig. 4.7a.
|
a b Fig. 4.7. Admissible ways of transition between the patterns of dynamic processes in the field from the view of classical physics (a) and relativistic conception (b); the red arrows show the transitions forbidden in classical conception
|
This diagram shows a clear distinction which the classical physics reveals between the motion of source and motion of frame. This is Newtonian separation into relative and absolute motions. The motion of the source of field can be in this meaning only absolute, and dependently on this motion the patterns transform. And the motion of frame is always relative, so this motion only shifts the pattern as the whole, while the pattern is determined by the state of motion of the source with respect to the luminiferous substance. The transformation of patterns done by the relativistic
conception we also can draw as some graph, see Fig. 4.7b. We see, the graphs 4.7a and 4.7b
are basically different. The above analysis shows, the relativistic conception uses the
transition F None the less, from the physical point even at the intermediate stage we see that relativistic transforms are artificial. In particular, when we showed in Fig. 4.2 the projection of propagation of equiphase surfaces, the Reader could note that the red markers denoting the projections of equiphase surfaces propagate with different speeds to both sides from the source. At the same time, in frames of relativistic formalism we can rigorously prove that these markers propagate in space with the same speed equal to the speed of light, and this is determined not by the speed of markers’ motion but by the inclination of a line along which the move in the plane (x', ct'), and this inclination is strongly equal to 45o . Actually, with the Lorentz transforms we can write |
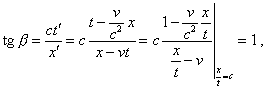 |
(4.25) |
where But the cause, why markers move with different speeds along this inclined plane of events, is that the laws of transform of time intervals are different due to the materialised time in the Lorentz transforms through the introduced spatial parameter x to the equation of time transform. True, this last did not much touch Einstein and his followers. “They juggle their symbols, while we in Cavendish obtain the unfeigned solid facts of nature”, – Rutherford [26, p. 541] said about it. For relativists “the theory of relativity is a perfect example of the modern way of development of fundamental theory. The initial hypotheses become more and more abstract, more and more far from being sensible. Instead, we more and more approach the most important target of science – from the least number of hypotheses or axioms to yield logically in deductive way the utmost real results. With it, the mental way from axioms to the sensible results becomes longer and longer and more exquisite” [27, p. 279]. But not in vain Einstein sought excuses on the way he went: “and we should not call the theoretician involved in this work the fictitious writer, reproaching him. No, better we approve his fantasies, as there is no other way at all to this aim (? – Authors). These are not idle fantasies, this is the search of logically simplest possibilities and their corollaries. This call for excuses was necessary, the listener or reader to be more inclined to follow with interest the below course of development of ideas” [27, p. 280]. Factually the way of Einstein and his followers was just to neglect the physical feature of phenomena for sake of mathematical beauty. Because of this, in particular, Relativity dared to violate the laws of transform of patterns of wave processes for sake of beauty with which the 4-D interval is written. With it, it denied the physical meaning of processes and retained only the reduced mathematical formulas cut off the phenomenological basis on which their derivations were based. Really, when, deriving the Lorentz transforms, Einstein writes: “… the light beam, in the measurement in resting frame, moves with respect to the origin of coordinate system k with the speed V - v due to which |
| (4.26) |
[4, p. 15], he, out of his wish, accounts the properties of interaction of the light wave with the resting luminiferous medium whose influence he rejects. The same, when he wrote: “Let at the moment of time tA the beam emerges from A, reflects at B at the moment of time tB and returns back to A at the moment of time t'A . Taking into account the principle of light speed constancy, we find |
| (4.27) |
where rAB is the length of moving rod measured in the resting frame” [4, p. 12], he also involuntarily accounts namely the wave properties of interaction of light with the luminiferous medium. With it, from the expressions (4. 27) which Einstein took from classical physics, there does not follow his conclusion: “We should not attach an absolute value to the concept of simultaneity. Two events simultaneous when observing from one coordinate system already are not taken in as simultaneous in consideration from the frame moving with respect to this frame” [4, p. 13]. Non-simultaneity takes place when we postulate the equal time spend by the light to pass from A to B and back, irrespectively of the state of motion of frame. But just to such result the relativistic expressions (4.10) and (4.23), yielded with the asymmetric transformation of time, come. So it would be incorrect to think the relativistic approach as the consequence of logical deduction from the regularities of nature, as Einstein tried to show it in the above citation. “In case of deductive derivation, the corollaries are in premises in a secret appearance, and they have to be taken of them due to the applied techniques of logical analysis” [28, p. 110]. In case of Relativity, the premises were not the general regularities of nature but an abstract hypothesis of constant speed of light in all frames that has no reflection in reality and only slightly resembles some outer revelations of physical processes. This likeness is so incomplete that with least refinement, the irrelevance causes paradoxes and requires to substitute further the physical meaning by mathematical symbols, and this marks the whole path of evolution of relativistic conception. While the basic postulate of constant speed of light in all frames was not substantiated then, when it was formulated in 1905, and it has not been substantiated up to now, and further evolution of relativistic conception caused formal rejection of this postulate. Well, if relativists think that in GRT the light-speed constancy is only local, this means, in the neighbourhood the light speed already differs from this constant. And even thought experiments in which they use reference frames moving with the sub-light-speeds, we in no way can squeeze into the concept ‘local’, if the time of any experiment multiplied into the speed of light is comparable with the size of gravitating bodies and, the more, exceeds the limits of homogeneous gravity potential. Einstein well understood, far from every statement can serve as the basis of physical conception. So he from the very beginning tried to substantiate the postulate, but having no direct proof, he made use of a trivial violation of logic, trying to prove the premise by its corollary. Actually, when relativists prove their postulate true,
they usually do it in one of two ways. Einstein used the first: “Let at the moment of time t
= |
| (4.28) |
Transform this equation with the above formulas of transformation (whose analogue in this our work is the conventional system of Lorentz equations (4.1) – Authors); then we yield |
| (4.29) |
Thus, the considered wave observed in the moving frame is also a spherical wave propagating with the speed V ” [4, p. 16]. The second way to prove was based also on the general system of Lorentz equations. In this way, relativists, basing on (4.1), find the differentials of coordinates and time in both frames, taking |
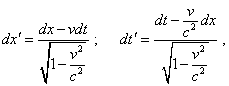 |
(4.30) |
from which, dividing the first equality into that second, they yield |
 |
(4.31) |
As we see, in both cases they use the Lorentz transforms in the most distracted appearance and prove the light speed constancy on whose basis they just yielded the Lorentz transforms. But if speaking, what occurs really and what is relevant to the studied properties of phenomena, there exist two ways to describe the processes of radiation/absorption. The first describes the radiation/absorption and motion of particles. In this case the speed of particle radiated by the moving source will generally be added to the speed of source (of course, if the mass of particle was well less than the mass of source). So, if we try to describe the time intervals for a particle in Einsteinian model, for the path from A to B we will yield |
| (4.32) |
or |
| (4.33) |
The same, for the back path from B to A, noting a fully elastic reflection from the massive barrier, yield |
| (4.34) |
or |
| (4.35) |
The expressions (4.33) and (4.35) show that if we sum the speed of particle with the speed of source, the time intervals for which the particle flies ahead and back are equal from the point of resting observer. The same, time intervals in the moving frame will be equal. Here we have to note, namely corpuscular representation of the light propagation, which Einstein veiled in SRT because of lack of redefinition of the properties of light, interrelates the relativistic conception with the photon conception built on the same epistemological principles – to reject the physical reality and to substitute the phenomenology of processes by the mathematical symbols, which is typical for the theory of relativity. At the same time, the speed of particle measured by the resting observer will show in the resting interval the summed speed of particle and speed of source, which would be surely discrepant to the initial postulates of independence of the light speed of the frame. This point of discrepancy was crucial for Einstein – not to redefine the properties of light, though in absence of aether as the luminiferous medium the corpuscular representation of light was the only logical consequence. The second way to describe relates to the processes in the medium. The point of this approach is that the equiphase surface radiated by the source propagates in the medium and obeys not the laws of source’s motion but the laws with which the excitation is passed by the medium. These can be mechanical, electrical, gravitational laws to transmit the excitation, but namely due to this transmission of excitation from the point to point, there arises the effect that the speed of wave propagation is independent of the speed of source motion that causes the constant speed of wave process propagation with respect to the medium. Just this approach leads the classical physics to the solutions (4.27) which Einstein took from the classical conception, substituting the corollaries. So, if we take away the medium in any its meaning or some properties, in this way we will violate the physics of process transmitting the excitation from point to point, as we took away the basis to transmit the excitations. Violating the physics of process, we deprive ourselves of our right to introduce the light speed independence of the pattern of source’s motion, and the very physical process of point-to-point transmission ‘hangs’, – just what we see in the relativistic conception. Extending this analysis onto the classical formalism, we can unambiguously conclude: the cause, why the Galilean frames are equivalent to describe the material points and non-equivalent to describe the field processes, is in different approaches to the description of particles that are material points on one hand and fields on the other. The classical conception still did not emphasise this feature; this made difficulties, of course, prevented to solve many problems, and, by the way, caused the creation of relativistic conception. But for classical physics it is not crucial – to reveal the difference between the transform of characteristics of particles and fields in transition from one inertial frame to another; this is unable to destroy the whole classical formalism, as classical transforms do not distort the plane of events. In this case it is definitive, as the basic properties of time remain. While in case of relativistic formalism, the shown improvement of the physics of processes destroys the whole relativistic tool, as, beginning with the postulates, the relativistic conception not only contradicts the physics of processes in dynamic fields but causes the corollaries fully contradicting the statement of problem in the very relativistic conception and the observed phenomena. As the result, the whole relativistic substantiation is factually reduced to the statement that “if we basically cannot measure the speed, in particular the speed of light, without some arbitrary assumptions, we may do arbitrary assumption also of the speed of light” [29, p. 181]. In this way relativists only emphasise that in building their conception they have incorrectly analysed the amount of known experimental methods whose aim was just to make the results free of arbitrary assumptions in passing from the particular studies to their generalisation, – what Newton just said and on whose basis he separated the concepts of relative and absolute. So it appears in the relativistic conception that “the question, is the Lorentz reduction real or not, is senseless. Reduction is not real, as it does not exist for the observer moving with the body; but it is real, as it can be basically proven by physical means for the observer who does not move with the body” [30, p. 187]. None the less, after analysing the classical and relativistic approaches to the description of field processes in reference frames, we have to admit that there exist two closed mathematical formalisms to describe the field processes. Both ways show formally closed logic in whose frames we basically cannot corroborate or disprove such or other mathematical tool. In particular, we see that relativistic transitions between F and G, though they are incorrect from the point of phenomenology of classical physics, mathematically rigorously transform one relation into another and vice versa. And this is quite expectable, as all transforms that we did, e.g., with the initial equations (4.2) were linear, and (4.2) as such were linear in x'a, y'a and t' , too. The same with (4.20) and (4.23). So we cannot think the yielded equations (4.10) and (4.23) as corroboration either disproof of relativistic conception. These solutions are within the same relativistic formalism as the initial expressions (4.2) and (4.20); so, being linear in their properties, they naturally satisfy all properties to which the Lorentz transformations are true. The same we understand, why the relativistic formalism is closed. The reason follows from the graph, as they take patterns F and G as the finite transforms. According to the calculation made in the section 3, in both patterns the speed of light propagation is constant, and the patterns F'' and G'' are basically transformed by the inclination of plane of events and factually are the intermediate chain between the patterns F and G. Due to this, the patterns of processes F'' and G'' have no independent meaning, just as the patterns F' and G' of classical formalism, as there is violated the condition of presence of physical time in the frame. Factually, relativists made their transition between F and G and here, if we disregard the physics that makes incorrect the very transition between F and G, the speed in both patterns is constant, which automatically satisfies the Einsteinian postulate. So it appears to be impossible to see the discrepancies of relativistic conception if we operate with the regularities which are the basis of formalism of this conception. This impossibility is like, for example, it is senseless to substantiate with help of usual trigonometry that the sum of triangle’s inner angles is 180o , because trigonometry itself is based on this equality and naturally will corroborate it true. Only leaving the equality of sum of triangle’s inner angles to 180o , we can hope to prove either disprove this statement which in its turn comes to the fifth Euclidean postulate of parallel lines. Just so all attempts to prove the fifth postulate in formalism of Euclidean geometry “did not reach the aim, as the problem was to make the Euclidean theory of parallel lines free of special postulate and, thus, the task here was not to substitute the fifth postulate by some other statement, even if it was quite obvious, but to prove this postulate, proceeding from the rest postulates of geometry” [31, p. 18]. The same with our solutions (4.10) and (4.23). To show that the properties of these solutions correspond to the real properties of space-time, it would not be enough to put the initial solutions (4.2) and (4.20) into agreement with the condition of presence of physical time in both frames. The very fact that relativists applied the Lorentz transforms predetermines the direction of transitions in the graph in Fig. 4.7b. To check, which of two formalisms reflects the reality, we have to compare these formalisms with the reality. The way to check is obvious. We saw, the classical formalism does not mean the pattern’s transformation in passing from the frame resting with respect to the luminiferous substance to that moving, while Einsteinian theory of relativity always means the transformation of pattern in such transitions. So, proceeding from Fig. 4.7, we have to check, how legal is to pass from one frame to another, and basing on, which structure of passing relates to the reality, we can judge, how legal is one either another formalism. To do the check with a good quality, we have to base our reasoning on the theses that are doubtless for both conceptions and to do not rely on judgements that are subject to check or are questionable. The first such point is the resting inertial frame with the source of light resting in it. If from the view of classical physics we premise as such frame some frame resting with respect of luminiferous medium, the modelling equations describing the equiphase surfaces for the relativistic resting frame and classical frame resting with respect to luminiferous substance will be identical. And in this model the speed of light propagation in both conceptions is same and isotropic. It means, we may take this model as the basis for our consideration. Further, we have to confine the consideration to one frame, as the discrepancies related to the non-simultaneity of events and consequences following from it on which the relativistic conception insists arise namely in passing between the frames. But we are interesting just to represent the equiphase surfaces from the point of moving frame; apparently, it surely will make us to arrange the moving frame. It appears, not always it is necessary. From the view of classical physics, we obviously do not need it, as in its formalism, space and the more time do not transform; only our measures can transform, which is non-adequate to the space-time transformation. So we can see processes in moving frames from the resting frame. But Relativity has to admit such possibility to see processes and transformations from the resting frame. In particular, we can recall Einstein’s phrase about reality of space-time transformation already cited above: “Reduction is not real, as it does not exist for the observer moving with the body; but it is real, as it can be basically proven by physical means for the observer who does not move with the body” [30, p. 187]. From this, if in the resting frame there exists the asymmetric transformation of equiphase surfaces, it has to be observable from the resting frame. Especially if we watch, how the information is mapped by the moving detecting device from the point of resting frame. We can use as such detector widely used in the scientific experimental practice a photographic plate which simultaneously maps the event on a definite plane by means of independently going chemical reactions. Lest to go into a rhetorical debates, whether the reactions go simultaneously from the point of moving observer, we will observe these reactions with the resting observer, noting the property of relativistic conception that it has to admit the evidence real if we have it already recorded. In particular, if we record by the photographic plate the pattern of equiphase surfaces in the moving frame and transmit this image to the resting observer, he may not consider this image from the view of relativistic non-simultaneity. The image is the fact for him, the same as for relativists the wave phase invariance is the fact, irrespectively of the frame: “the phase has to be invariant” [23, p. 36]. With the same success we may map the image onto a moving photographic plate and present it to the moving observer. And this will be the fact for him, too. In this second case, the image on the plate has to be identical with the image obtained by the moving observer, if the speed and direction of motion coincide with the speed and direction of this observer. Thus, studying the process, how the equiphase surfaces are detected from the point of resting observer, we evade the necessity to pass to the moving frame and can determine the basic fact: do the equiphase surfaces transform in the moving frame or not, and, consequently, reveal the physical truth of such or other conception. To do so in the most correct way, we will proceed from the doubtless, in this case, fact that the equiphase surfaces in the resting frame have the shape of concentric rings. Hence, if on the way of light propagation we arrange the ring-shaped hold elements, they will reflect the geometry of equiphase surfaces. Proceeding from this, let us take some cylindrical pulsed source of light and arrange around it the conic semi-opaque reflectors that allow some part of the light signal to pass to the next reflectors, and a part of light wave they will deflect perpendicularly to the light propagation. Let us choose the size of conic reflectors so that the between-rings distance was equal to the product of the light speed into the pulse period. It is easy to see that such scheme models the momentary pattern of equiphase surfaces. And conic reflectors are not the only solution of problem. We can put on their place sensors which would detect the wave phase (or, in case of our pulsed source, to detect the pulse of light) and emit the pulse of light onto the photoplate at the moment when the phase detected. The result would be same. Further, let us put the detecting photoplate so that it moved with some speed above the set of conic reflectors at some height h, as it is shown in Fig. 4.8. |
Fig. 4.8. The scheme modelling the pattern of equiphase surfaces in the resting frame
|
We see from Fig. 4.8 that all beams reflected by the conic mirrors will reach the photoplate simultaneously – of course, from the point of resting observer, which is enough for the considered scheme. Reaching the photoplate, the beams initiate chemical reactions, mapping on the plate not relative but absolute pattern. Irrespectively of, whether moving observer sees the light reaching the plate simultaneously or not, he can see only the result of chemical reaction that does not depend on the relativistic non-simultaneity, since it reveals itself as the fact of blacked crystals of photoemulsion at definite places of plate. The blacked places also will not depend on, whether the plate changed its longitudinal size. In case of such shrinkage, this size has to change for all regions and is able only to transform the circles into ellipses but cannot transform the concentric circles into some asymmetrically arranged ones. But if the relativistic approach is true, we have to expect just this – and we have not to, if the classical modelling is true. So we will model the process from the point of resting observer to check, will it develop an asymmetric pattern or not. The result is shown in Fig. 4.9.
|
Fig. 4.9. The model to detect the equiphase surfaces by the conic reflectors from the point of resting frame, with the speed of photoplate v = 0,8 c
|
The diagram shows that the independent detection gives the pattern of non-transformed equiphase surfaces; from this, the classical modelling is true. We have to underline here that, diminishing the height h to zero, we pass from the mediated to the immediate detection of equiphase surfaces, and the whole time while we diminish h the pattern will not change. Consequently, in the limit, in the immediate detection of equiphase surfaces, we will also see the non-distorted pattern corroborating the classical formalism true. This pattern will be the reality independent of the observer. If, suppose, the moving observer tries to detect the mutual location of rings with his measures of length, in premise that they transformed, he will not see the asymmetry of rings which is absent, while according to the relativistic conception, he has to see this asymmetry. We can predict that adherents of Einsteinian theory try to imagine the map not on the horizontal plane of events related to the simultaneous detection of equiphase surfaces but on the inclined relativistic plane of events. To prevent these attempts to squeeze the simultaneity into physics, recall the rules, how equiphase surfaces form: each equiphase surface is radiated by the source one period earlier than the enclosed equiphase surface. Consequently, if in the light pulse we additionally transmit the code of radiation time, on all concentric surfaces detected by the plate we will see the detected time decreasing in a clear accordance with the radiation period. We can use these data to synchronise the physical time in the frame of moving observer – and we will see the simultaneous detection. To the point, if we, following the relativists, neglect the features of physical processes, we can, basing on the data of these images of equiphase surfaces, plot another surface of simultaneity; it will conically expand from the central equiphase surfaces to that peripheral. This will be already not the inclined surface, but basing on this ‘cone of non-simultaneity’, we can also plot some internally closed mathematical nucleus. However, this nucleus will be true only in the limits in which it was built, and will be limited by the laws of measuring scheme on which it was based. If we change the scheme, the measurement conditions will change, and the mathematical nucleus will give paradoxical results. In the considered case of marked maps of equiphase surfaces, if we put, as above, instead the conic reflectors – the detectors of phase with synch radiators, then, given the possibility to synch the clocks joined with each sensor in the resting frame, we will yield already another marking of equiphase surfaces on the plate. This marking will determine the horizontal plane of events, as all markers will come into action and the light from them, from the point of resting frame, will reach the plate simultaneously – consequently, the moment of detection will be one and the same. And the very fact that we can give to some region of the moving frame the physical time from another frame, and just with the light beams, says that relativistic non-simultaneity is not the physical phenomenon but one of the first paradoxes which Einstein encountered and, having no wish to reject the abstract mathematical nucleus, without grounds called it physical phenomenon instead to clarify the statement of problem that immediately showed to Einstein the paradoxical pattern of the inclined plane of events and that the non-simultaneity of events in no way can be the cause – it is the consequence of postulating of light speed constancy in all frames. So we can surely state that the cause of non-simultaneity and other paradoxes of Einsteinian SRT is not the indefinite physical phenomena – the particular has been illegally generalised through the generalisation of mathematical expressions built on the particular effect or measurement scheme. While the feature of mathematics, in the common understanding of scope of this tool, is that the mathematical scope is much wider than we need to describe the physics of phenomena. It is able to produce multitude of versions, the more if we apply it to an incomplete or intentionally limited in our formulation phenomenological basis. For example, neglecting the fact of strongly positive values of mass, we are mathematically able to take the mass negative or even complex in the Newton second law and this will not contradict our operations. We can form so an internally closed mathematical conception which in its particular results will be true for the observed phenomena. The same we can take negative the frequency of process and will yield mathematically consistent results. We can give many other examples, just as many ‘theories of everything’ that are developed now; they all are based not on the utmost information of phenomena but only on some part convenient to build a non-contradictive mathematics. All these conceptions have in common that in each case such or other property of phenomenon is ignored; for example, relativists ignore one direction of time. Or, as we saw above, they lift the basic limitation of possible passing between the patterns of field processes that admit the passing from the pattern F to the pattern G. And often, if we take an exceptionally mathematical point of view, formally nothing prevents us to interrelate the physically incorrect transitions, the same as to introduce some 32-D physical space, to curve the time, to incline the axis of events etc. But side by side with impeccable mathematical consistency, in such conceptions the paradoxical results will arise; the collision of results yielded in an abstract way with the experience causes it, because just it produces paradoxes, as for example in case of negative mass the body will move against the affecting force. Or as in the Einstein theory: “the law of parallelogram of speeds is in our theory true only in the first approximation” [4, p. 20]. To say exactly, just in the approximation when they can neglect the relativistic multipliers, passing to the formalism of classical physics. The same we will yield that the gravity interaction can be not only attractive but also repelling, and we will come to the negative kinetic energy of bodies. We can differently interpret these paradoxes, but at the next step these interpretations will show themselves wrong and we will have to seek new treatments for new revelations, or neglect again the properties of studied phenomena, as these new treatments will contradict those previous, since paradoxes arise just when the interpretation is unable to substantiate the complete amount of observed phenomena but explain only a part of observed properties. Then the interpretation unavoidably contradicts other revelations. This is the more typical when the observed physical properties are squeezed into the limits of some abstract mathematical description or postulate. A typical example is the stellar aberration. In its essence, this is the difference between the angle under which we see the star and the angle of inclination of quadrant, sextant or telescope. Yes, these are main astronomic devices which people use to observe stars; they all are based on the common idea of coincidence of view-finders, which just causes the aberration. And this is an important feature that separates the idea of physical basis of aberration as the parasitic phenomenon arising in observation by a definite technique from the physical properties of celestial objects, in particular – from the properties of space. But with time, this feature was omitted, and now we read in the encyclopaedia: “The light aberration (in astronomy) is the change of visible location of the heavenly body on the celestial sphere caused by the finite speed of light and observer’s motion due to the Earth’s rotation (daily light aberration), Earth’s orbiting around the Sun (yearly light aberration) and travelling of the Sun system in space (celestial light aberration)” [32, p. 9]. Thus, the cause of stellar aberration has been factually substituted by the condition determining the regularity of its change. With it, we cannot deny that the aberration does not relate to the speed of observer’s motion. The cause of aberration is not the motion but necessity to superimpose the view-finders. It arises from the necessity to superimpose the markers distanced from each other, but the very between-markers distance is cancelled in mathematical operation, only the dependence on body’s motion remains, i.e. the secondary cause that will not reveal itself without the primary cause. Because of this inaccuracy in the definition, in the relativistic conception this makes the stellar aberration already an inalienable part of space-time distortion and, passing from the undotted to dotted polar angles, we factually used the relativistic formula of aberration (4.15), as the angular measures in the relativistic conception are distorted just due to mutual motion of frames, not due to the necessity to superimpose the view-finders. Factually, this formula is irrelevant to phenomena in space, since, as we already said, the aberration is exceptionally an instrumental error, and if we use the technique of angular measurements without superimposition of view-finders but through, e.g., simultaneous stereo-shooting of two stars, the angle of one of which was given either preliminary found, the aberration will not arise, as its cause will be lifted before the observation. While in the relativistic conception the aberration will remain, as its physical meaning has been separated from the mathematical tool and is already defined not by the instrumental technique of measurement but by some physical phenomena separated from measurement and from the observation at all. As the consequence, there arise the paradoxes like deformation of equiphase surfaces with the angle ahead which we showed in Fig. 4.3 and 4.5. The study which we made in this section shows that the closed mathematical nucleus as such does not corroborate the physical conception correct. To describe the phenomena truly, the physical conception has to contain the complete information in its basic principles on whose the mathematical nucleus is formed. And these principles have to be exhaustively checked in the experimental study of phenomena. Namely complete and correct account of basic properties of phenomena can ensure correct mathematical description from the view, is it associative with the physics of phenomena or not. From this view, it would be interesting to analyse the geometrisation of physical phenomena that relativists made on the grounds of joined spatial and time characteristics of description of physical processes, as here we also will encounter some formally closed mathematical nucleus and non-associative basis on which this nucleus has been formed. |
Contents: / 53 / 54 / 55 / 56 / 57 / 58 / 59 / 60 / 61 / 62 / 63 / 64 / 65 / 66 / 67 / 68 / 69 / 70 / 71 / 72 / 73 / 74 / 75 / 76 / 77 / 78 / 79 / 80 / 81 / 82 / 83 /