SELF |
64 |
S.B. Karavashkin and O.N. Karavashkina |
|
|
|
SELF |
64 |
S.B. Karavashkin and O.N. Karavashkina |
|
|
|
As another typical example of corrupted mathematical formalism for sake of wholeness of some mathematical nucleus of the Einsteinian theory of relativity, we can recall the mythical turn of coordinate system by the imaginary angle; relativists widely use it in their works. Basically, we already discussed this issue in [11, p. 37] and showed, this operation is factually not a turn but a transformation of coordinate system. So the relativistic predictions made with the imaginary turn usually do not coincide with real results even in their conception. So we will consider here not so much the fact of coordinate system transformation but will show the point where relativists, in their abstract geometrisation, based on the outward likeness, violating the mathematical formalism. Let us follow for it the substantiation of the complex
angle of turn which, as relativists say, implements the Lorentz transform. “Let us make sure that the turn transform in the 4-D space (x, y, z, |
| (5.4) |
| (5.5) |
(where |
| (5.6) |
Having divided the upper expression by that lower, yield |
or |
| (5.7) |
where v is the speed of
uniform motion of the origin of coordinate system K' (point x'
= 0) relative to the coordinate system K. From the equality (5.7) we can easily
find the values of sin |
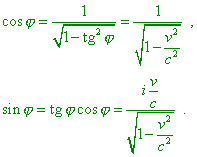 |
(5.8) |
With it |
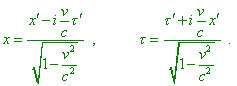 |
(5.9) |
Passing from |
Fig. 5.5. Graphical interpretation of Lorentz transforms
through the turn of the coordinate system by the imaginary angle
|
It would be not excessive to underline the conventional pattern of graphical appearance of the Lorentz transforms. The turn angle in Fig. 5.5 is imaginary. Of course, we cannot draw the turn by the imaginary angle” [53, p. 215–216]. Analysing this derivation, let us first of all draw our attention to Fig. 5.5 and make sure, relativists in their graphical interpretation actually turn the axes, while we remember, in the statement of problem they said, “the motion of inertial systems of coordinates occurs in direction of joined axes x and x' ” [53, p. 215]. And this stipulation is required not only for the geometric interpretation. The coincidence of axes is the basic stipulation in Einstein’s derivation of Lorentz transforms: “Let in the ‘resting’ space two coordinate systems are given, each with three mutually perpendicular axes starting from one point. Let the axes X of both systems coincide, and axes Y and Z are parallel, respectively” [4, p. 13]. Proceeding from namely this condition, Einstein wrote: “hence, three sought formulas of transforms have to have the appearance |
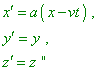 |
(5.10) |
[52, p. 71]. Should two axes were really inclined to each other, the first expression of the system (5.10) would have basically another appearance, namely – |
| (5.11) |
the further Einstein’s derivation would take absolutely other way and would lead him to the absolutely other result, as (5.11) is basically other than the first equation of (5.10). These equations to be equivalent, it is necessary, |
| (5.12) |
to be true, or the coefficients at x and t in (5.10) will not correspond to the trigonometric functions. As the result, we see this in the above derivation. Actually, according to the first equation of (5.8), the cosine of angle is a real function whose value is more than one in the whole range where the speed v of frame varies from zero to the speed of light. But then it is already not the trigonometric function, and hence, the geometric interpretation as the turn of axes is incorrect. The same concerns the sine of imaginary angle of turn. If the trigonometric cosine is a real number, the sine of this argument in no way can be a complex number, noting that according to the basic theorem of trigonometry |
| (5.13) |
While the sine in (5.13) is imaginary, this directly follows from the violation of the expression of sine that makes it more than one. Thus, one violation brings another. Factually, the operation relativists did is like this: |
| (5.14) |
where |
We see from (5.14) that the real number is written as some pseudo-complex transform that contains the same imaginary tangent of the argument. And imaginary tangent does not mean the imaginary argument. But out of any doubt, the imaginary value of tangent of some angle is a gross violation of mathematical formalism. With it, the initial number in (5.14) did not become complex, as well as it is impossible generally to express the real number as a complex number with a non-zero imaginary part. But relativists do so and yield incorrect geometric interpretation, discrepant statement of problem, full opposition of their mathematical nucleus to the mathematical formalism. If relativists had a wish to introduce some analogy with the turn of coordinate axes in accordance with the mathematical formalism that in many centuries of study proved itself associative in modelling of physical processes, the transformation of the initial Lorentz formulas has to be the following: For the spatial coordinate |
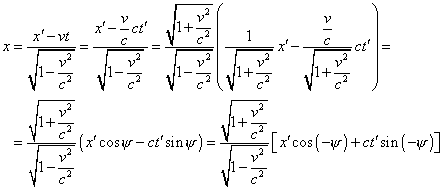 |
(5.15) |
and for the time transform |
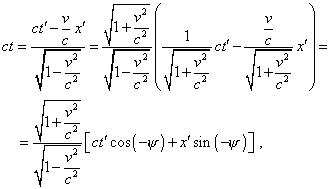 |
(5.16) |
where |
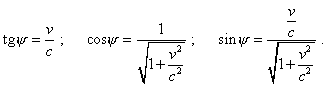 |
As we see, in frames of mathematical formalism, i.e. when we keep the rules of transforms, the angles are real, the values of sine and cosine are in agreement with the trigonometric properties, and the transform turns the plane by an absolutely real angle, noting the additional mirror map. We also see in the denominators the sum, not difference, which is in agreement with the condition (5.12) that provided the correctness of operations with trigonometrical functions. And this is the reality that is revealed in the diagrams we showed, as the time component becomes dependent on the spatial parameters and, consequently, we see the inclination of the plane of events, and the properties of time, becoming ‘tangible’ and including simultaneously existing spatial parts, come to contradiction with their definition. To the point, from the transforms (5.15) and (5.16) we can yield the expression for summation of speeds, similarly to the relativistic version of (5.7), noting the requirement that has been put into the condition (5.12). Actually, |
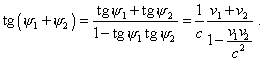 |
(5.17) |
True, as the transforms violate the basic property of time, the law of adding speeds also contradicts the physics of processes making it ambiguous, – we will show it in the subsection 7.1, in special consideration of this issue. But what cannot give this correct transform with the turn of axes is the complex pattern of 4-D interval. In this connection, relativists artificially introduced the complex unity – initially to the 4-D interval, then determining the angle of turn of axes. In this way they did one more important violation of mathematical formalism, of which we said in details in [12]. Thus, we see that corruption of physical processes in construction of relativistic conception required to corrupt adequately the mathematical formalism, making the closed mathematical nucleus true only in some amount of abstract, physically non-associative operations, both in their main derivations and in the corollaries, bringing the relativistic conception to the paradoxical geometry. Namely so all derivations on which relativists base relate either to some hardly checkable phenomena or to the existing definitions which they can doubt as untrustworthy observations with limited facilities or in absence of full information, or because the technique of study relates to the specific scheme on whose grounds relativists developed their conception. When broadening the research scope, Einsteinian conception automatically becomes inconsistent both with itself and with the observed phenomena. It follows from this analysis that the 4-D multiplicity of Einsteinian theory disregards the physical properties of time. This disables to operate in frames of joint space-time, the more to substitute the physical interactions in fields by their imaginary curving or imaginary turn of axes without their real turn, due to the statement of problem that even cannot be defined without violation of the phenomenology of physical processes and basic mathematical formalism. |
Contents: / 53 / 54 / 55 / 56 / 57 / 58 / 59 / 60 / 61 / 62 / 63 / 64 / 65 / 66 / 67 / 68 / 69 / 70 / 71 / 72 / 73 / 74 / 75 / 76 / 77 / 78 / 79 / 80 / 81 / 82 / 83 /