V.6 No 1 |
75 |
| The problem of physical time in today physics | |
|
|
V.6 No 1 |
75 |
| The problem of physical time in today physics | |
|
|
7. On possibility to transform the physical time in reference frames moving with the sub-light speed In the previous sections we described in details the main properties of time from the view of today physics and showed the geometrisation of time to be incorrect. Time by its definition may not be geometrised, because its parts do not coexist in space. The fact that researchers plot graphs for their experiments and calculations with the time axis does not mean that we materialise time. As opposite to space to whose points we can return in some or other way, time flows strongly from past to future and all repetitions will occur already in other time. We also have cleared that among multitude of reference frames, there exists a selected frame that, realised or not, is present both in classical and relativistic derivations. It differs from others so that the light propagation is isotropic in it and the transformation of equiphase surfaces is transferred to all other frames that are moving relative to this selected. Now, to clear the issue of possible transform of time, we have to join the revealed amount of knowledge with the concept of possibility to transform the very time. 7.1. Transform of time in the relativistic conception Keeping the sequence of consideration, we have first to analyse, how much real is it – to transform time in the relativistic conception which has conceptually stated that time is changed in frame-to-frame passing. “It is always asked, ‘Is the Lorentz transform real?’. The doubt arises usually because the length of moving bodies is determined arbitrarily in the measure in which the conventional definition of simultaneity (e.g., Einsteinian, which we use) is arbitrary. But we can definitively answer, this phenomenon is real, as one and the same procedure of length measurement will give different results in classical (Newtonian) theory and theory of relativity” [24, p. 64]. “… The spatial and temporal data have not fictitious but physically real meaning. In particular, it concerns to all relationships that include coordinates and time…” [81, p. 24]. Of course, speaking of relative measurements, we involve some ambiguity, because we think the shapes and motions of material bodies projectively – often not only due to speed of material bodies in space but also due to different temperature, pressure of environment, affection of different fields, the angle under which we observe etc. These effects are well known in metrology; they can be imaginary – caused by distortion of our measures or spatial distortions, – either real, if we measure, e.g., the length of heated rod or the frequency of signal radiated by the moving source. Anyway, we cannot attribute these transformations to the transformations of space-time, as they result from affection of certain factors both on the subject of our measurements and on the measure with which we try to make measurements. In other words, we anyway are speaking of something quite particular which we may not extend, making of it a property of the whole universe, of all measurements and all measured bodies. So in measurement of both time and lengths, metrology accounts these affections, relying namely on the knowledge of physical laws. To their techniques to avoid the distortions that usually are caused by systematics, “… we can attribute first of all the previous study of errors and introduction of related corrections, i.e. the premature check of all measuring instruments, finding the coefficients of correction and effect on the readings of different external factors” [82, p. 19–20]. In this connection, the very fact that the procedure of measurement of lengths after Newton and Einstein gives different results is not the evidence that such or other technique of measurement is true. We have to consider the techniques with the whole amount and correctness of ways, how they account the affecting factors. Relativists substantiate the time contraction in moving frames so: “… Now let us address to a similar problem for the time intervals… In particular, we have to find the pace of moving clocks. Suppose, the standard clocks resting in the frame S' send signals each second; which will be the interval between these signals in the frame S? To apply the Lorentz transforms to this problem, we have to interrelate some events with signals. Such events can be the switches of a lamp connected to the clock and driven by its mechanism. Sequential readings of an arrow on the face against 12 hours, 12 hours 1 sec., 12 hours 2 sec. and so on also can be the events. Each such event detects the location of clocks in space at the moment of their existence. If in the frame S' the clock is at the point (x', y', z') , then two sequential signals from them will correspond to the events with the coordinates (x', y', z', T') and (x', y', z', T' + 1) , where T' is some number. According to (2.10) (the Lorentz transforms in general appearance (4.1) – Authors), the moments of same events are written in the frame S as |
| (7.1) |
| (7.2) |
and the subtraction gives, from this, |
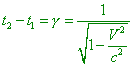 |
(7.3) |
(in seconds). This is just the sought interval of time in the frame S. It exceeds one second, so the moving clock seems to be going slower (loses). From the symmetry (equivalence of frames), it follows that the standard clock resting in the frame S look like losing in the frame S' , we can make sure in it immediately from the law of transform. Just as in case of mutual shortening of lengths, there is no contradiction. In one case, a particular clock from the frame S' is compared with the sequence of clocks of the frame S that appear in the near of it and that all are synched with each other through the Einsteinian procedure taken for S. In other case the particular clock from S is compared with the sequence of clocks from S' that are synched by Einsteinian procedure but applying to the frame S' . The moving clock loses. This effect is called the deceleration of time” [24, p. 64–66]. In the Einsteinian interpretation, the same procedure to compare the intervals of time in the mutually moving frames sounds the same: “Let in the coordinate origin of the frame K' there is the clock with a second arm. For it, x' = 0 always, and it counts its seconds at the moments of time t' = 0, 1, 2, 3 etc. The first and fourth equations of transform give for the time t of these second readings the values |
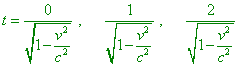 |
(7.4) |
etc. Thus, in the frame K the time between the readings of clock is |
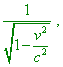 |
(7.5) |
i.e. more than a second. The clock moving with the speed v goes – from the point of non-accompanying coordinate system – slower than this same clock would go, should it was resting” [45, p. 420]. Thus, Marder’s conclusion is in full accordance with Einstein’s conclusions; so we have to attribute all discrepancies that arise in this approach to compare the pace of time not to Marder’s interpretation but to the very relativistic representation. And there are the discrepancies, despite relativists insist that “there is no discrepancies”, and they are namely in the full equivalence of frames, which is the basic postulate of SRT. To reveal sequentially the whole amount of arising discrepancies, consider this matter sequentially. 7.1.1. The problem of mutual contraction of time intervals We have to draw attention to an important point of clocks check. Einstein writes: “… The clock moving with the speed v goes – from the point of non-accompanying coordinate system – slower than this same clock would go, should it was resting” [45, p. 420]. Marder writes the same: “ The moving clock loses”. It remains only to clear up, which of two clocks move? The more that each clock moves relative to another frame but rests in that accompanying. From this, if one clock goes slower relative to another, then, with fully identical frames, the clock of another frame, too, has to go slower than from the point of non-accompanying frame. The formulas of Lorentz transforms corroborate it. Noting that the speed of moving frame is squared in (7.3) and (7.5), when substituting the primed symbols to those unprimed, we will yield the same result. This means, it is impossible to introduce the difference between frames, remaining them inertial and relativistically identical. And when Marder tried to compose the scheme of synchronisation as follows: “In one case, a particular clock from the frame S' is compared with the sequence of clocks of the frame S that appear in the near of it and that all are synched with each other through the Einsteinian procedure taken for S. In other case, the particular clock from S is compared with the sequence of clocks from S' that are synched by Einsteinian procedure but applied to the frame S' ” [24, p. 66], – it did not help to solve the problem. From the fact that each clock synchs the time intervals after its own procedure, it does not follow that in one case the clock will lose but in another will go faster. The measurements made by the same procedure from S to S' will show the same dilation as the measurements from S' to S, and we will come to conclusion that the shortening is imaginary. Not in vain Einstein in his paper on the twin paradox disproves Marder’s statement, long before Marder wrote it: Critic: … Even the most zealous adherents of the theory will not state that each of two clocks resting near each other lose comparing each other. Relativist: Your last statement is true beyond all doubts, but the way you derived it is not true, because, according to the special theory of relativity, the coordinate systems K and K' in no way are equivalent. Actually, this theory states equivalent only all Galilean (non-accelerated) coordinate systems, i.e., such coordinate systems relative to which enough isolated material points move rectilinearly and uniformly. Such coordinate system is K, of course (from where the twin starts – Authors), not the system K' that is from time to time accelerated” [83, p. 618]. Thus, according to Einstein, the reality of space-time transform is caused, none the less, not by Lorentz transforms as such but by the fact that one of frames once has been accelerated (i.e., again, by non-equivalence of frames). The time deceleration of the twin that flied away is proportional not to the periods of acceleration/deceleration but to the full time in which the inertial sections are much larger than those non-inertial, and the main, we can give them an absolutely arbitrary duration. Proceeding from this, relativists think that the acceleration in the pre-history of each inertial section not so much introduces a correction to the clock’s reading as interrelates the time shortening to the accelerated frame. And from this, it follows that if the twins synchronously accelerate/decelerate in different directions from the initially common inertial frame, there will be no time difference when they return to the initial point. At the same time, if on their synchronous inertial sections they check their clocks, one of them has to appear younger, as in the derivation of transforms which Einstein multiply repeated, beginning from the paper of 1905 [4], the main aspect of affection of pre-history of accelerated motion onto the time transform has not been mentioned, and Lorentz time transform has been derived for the mutually moving inertial frames, irrespectively of something else. According to the relativistic statement of problem, “If we leave aside the trivial kinematics and create a new one, on new principles, there will arise the transform formulas different from the shown above. Thus, now we will show that from the 1. Principle of relativity 2. Principle of lightspeed constancy there follow the transform formulas allowing to see that the Lorentz theory is compatible with the principle of relativity. The theory based on these principles we call the theory of relativity” [17, p. 152]. Thus, the whole derivation of transform formulas is based only on two postulates, and the postulate of relativity in the relativistic interpretation means that “the laws that drive the phenomena of nature do not depend on the state of motion of the coordinate system relative to which these phenomena are observed, if this system moves without acceleration” [17, p. 145]. And here also he says nothing of the pre-history of inertial frame and requires only, it to be not accelerated at the moment (which Einstein disproved later, having introduced a full equivalence of all frames). But in this case the fact remains. If the time transform is real only in case if one of frames was accelerated, it has to be seen in the proof which Einstein multiply did, the more that, if the theory of relativity considers the transforms between mutually moving frames, the mutual motion to begin, one of frames or both some time in the past had to be accelerated relative to each other. This means, the fact of acceleration has to be present in the substantiation of conception and factually has to substitute the principle of full equivalence of frames, selecting among the mutually moving frames that which did not accelerate. But if the reality of shortening follows from the above mentioned postulates of SRT, then with the full identity of frames, this shortening is imaginary, just due to this full identity that is explicitly present in Einstein’s proof. |
Contents: / 53 / 54 / 55 / 56 / 57 / 58 / 59 / 60 / 61 / 62 / 63 / 64 / 65 / 66 / 67 / 68 / 69 / 70 / 71 / 72 / 73 / 74 / 75 / 76 / 77 / 78 / 79 / 80 / 81 / 82 / 83 /