SELF |
82 |
S.B. Karavashkin and O.N. Karavashkina |
|
|
|
SELF |
82 |
S.B. Karavashkin and O.N. Karavashkina |
|
|
|
7.3. The features of transformation of absolute and relative measures In the previous section we could see that the development of technique of measurements went from quantitative definitions to the relative measures and via them – to those absolute. During this process, the passing from qualitative to quantitative measures was factually defined by the necessity of clearer gradation of the measured value. Gradation also started not from a number but from the concept ‘more – less’ and then the difference was redefined and the concept of quantity of unit measures included into the measured property of object shaped. In its turn, the main reason, why the absolute unit measures were sought, was that relative measures are subject of external affections, because the very material bodies whose properties are taken as the unity of measure are the carriers of relative measures. So the external affection is reflected not only on the measured object but on the carrier of measure. As the transformation of properties under affection of external factors depends on the properties of material of the carrier of measure, the error of measurement depends on, how the properties of carrier of measure agree with the properties of material of the measured object. If they are same, distortions will be least, but they grow fast if the measure and object are much different in their physical characteristics. This feature is inherent in practically all measurements, not only in properties of material bodies moving with the near-light speed.
|
Fig. 7.10. The virtual temperature transformation of space due to the thermal expansion of the measure
|
For example, take two identical measures and place them in two thermostats so that in one of them the temperature is hotter and in another colder comparing the environment, as it is shown in Fig. 7.10. Then, according to our experience, in the cold thermostat the measure becomes shorter and in that hotter it becomes longer. Does it mean that the space in thermostats has transformed? Not of course. To make sure, we can measure the thermostats by the outer measures that are at the temperature of environment. So we will reveal that the outer size of space surrounding the changed measures remains same, irrespectively of, whether the carriers of measure are inside them or not, and of, which temperatures are in the thermostats. Hence, the transformation is inherent in the very carriers of measures, not in the surrounding space. And this feature is typical for relative measures. Not the space but our calculus of space changes, and these are different things. The same, we can place to the thermostats mechanical clocks and make sure that the pace of time in the hot thermostat differs from that in the cold thermostat. Does it mean that the time in the selected areas of space has changed its pace due to the hotter or colder conditions? Undoubtedly not. There have changed the parameters of used carriers of measures, not the time as such; from this we see that it is incorrect to identify the measures of space and time with our material carrier of measure. Possibly, it will seem to the reader that it is incorrect to compare the relativistic contraction with that thermal, but let us see into the origin of SRT. If someone is sure that it was based on the postulates of relativity and constant speed of light, he misleads himself. These postulates continued the mathematical manipulations with the formulas that described the Michelson – Morley experiment in an exaggerated way. “Before we approach the essence of theory of relativity, I (Einstein – Authors) would like to underline, this theory originated not in speculative way but due to the striving to satisfy best the experimental data. Here we have not at all a revolutionary fact but natural continuation of the line of development going through the centuries” [91, p. 109]. “Recall the considerations on which the experiment by Michelson and Morley has been based. As we have revealed, the times spent by the lightbeam to pass the distance l ahead and back differ dependently of, whether the light propagates in parallel either in perpendicular to the direction of Earth’s motion. In the first case |
| (7.64) |
in the second |
| (7.65) |
If now we suppose that the arm of interferometer directed in parallel to the Earth’s motion has been shortened in relation |
the time t1 appears lessened in the same proportion, i.e. |
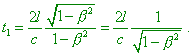 |
(7.66) |
With it we would yield t1 = t2 . The hypothesis follows from this (whose lack of grounds and liberty are really striking): every body whose speed relative to the ether is v is shortened in the direction of motion by |
[97, p. 214]. Doing not going into details of, how much the mathematical
expressions (7.64) and (7.65) agree with the calculation formulas of real MMX whose
incorrectness has been shown to Michelson and Lorentz by their colleagues at the Pasadena
conference (in more details see our paper [15, ?. 53]),
we will concentrate on the issue of our present interest. It follows immediately from the
citation that according to the Fitzgerald hypothesis, there has been deformed the
longitudinal arm of interferometer, not the longitudinal component of the universe. It is
important that the time does not contract in this scheme. The value of time which the beam
spends to pass the longitudinal and transverse paths (7.66) has the same appearance as in
classical calculations, only supplemented by the contraction of longitudinal arm of
interferometer, as the expressions (7.64) and (7.65) have been written from the point of
resting frame. So in the expression for time (7.66), the relativistic multiplier (1 - The same in Lorentz’ interpretation: “Basing on the theory, due to the forward motion, the time during which one beam goes along P ahead and back increases by |
| (7.67) |
comparing with the time during which another beam passes its path. The same difference would take place, should, in case of absent affection of forward motion, the arm P be longer than the arm Q by |
The same consideration is applicable for the second main position. Thus, we see that the phase differences expected by the theory could arise also, if in the rotation of instrument, once one arm, once another would be longer. Hence, these phase differences can be compensated by the reverse changes of sizes” [98, p. 12]. In other words, in both cases we are speaking of transformation of arms of interferometer, i.e. of relative measures, not of the space and time as such. The possibility of such transformations of carriers of measures is quite real, if we recall the deformation of fields of atoms. On the other hand, as Miller marked, in this case we may not speak of equal deformation of any materials, as each material of which the arm of interferometer can be done will transform dependently on its crystal, amorphous or fibrous structure: “In 1895, Lorentz and Fitzgerald premised that the motions related to the transfer of a solid body through the ether can cause the shortening of their size in the direction of motion and lengthening of sizes in the perpendicular direction; the changes are proportional to the squared ratio of the speed of motion to that of light, so that they ‘zero’ the effect of ether wind in the Michelson – Morley interferometer. The optical size of the instrument has been determined by the physical properties of sandstone of which the base of interferometer was made. Should the size shortening depended on physical properties of solid body, we could suppose that the pinewood beam would encounter larger contraction than the sandstone, and steel would shorten less. If the contraction puts to zero the effect in one instrument, the effect in another instrument will be non-zero and, possibly, having another sign” [99, p. 74–75]. In this case it had no sense to suppose that “we had only to understand that the auxiliary value introduced by H.A. Lorentz and called ‘local time’ we actually had to define as ‘time’. With such definition of time, the main equations of Lorentz theory will satisfy the principle of relativity, if we substitute the above transforms by other equations related to the new concept of time” [52, p. 66]. As we could see, in the Fitzgerald hypothesis, as well as in the initial Lorentz hypothesis, the issue is not the frame-to-frame time transform but only that from the point of resting frame, with the physical shortening of longitudinal arm of interferometer moving relative to this frame, there disappears the difference of time which the beam takes to pass the longitudinal and transverse paths, and nothing else. So the hypothesis of shortened longitudinal arm of interferometer needed no new idea of time and the more of its transformation. And relativists, with all their statements of shortening of space and time, transform by their transforms also factually the relative material carriers of measure, not space as such. “In the theory of relativity, since it does not admit the ether, this premise (of Fitzgerald shortening – Authors) is senseless, of course. But in the view of non-classical change of coordinates of events in passing from one reference frame to another, we can expect that the size of bodies has to differ in some way, from the view of different frames. It is easy to check it as the coordinates and process of measurement are tightly interrelated” [24, p. 62]. “Einstein’s postulate was not trivial, as it first was formulated to measure lengths with help of rods. Note also that in the experiments by Michelson – Morley and Kennedy – Torndike, the distance between separate parts of devices actually are determined by rods” [24, p. 45]. Furthermore, it is easy to prove the impossibility to transform the space, changing the parameters of motion of the relative frame, in the same way as we used it in case of temperatures. Actually, suppose, we have a possibility to isolate quite large region of space (e.g., several parsecs), and let in this selected region we have some inertial frame moving with the near-light speed relative to the resting frame related to the selected region. Thus, the observers in the moving frame have a possibility to measure the selected volume from inside, and the observers in the resting frame measure the same volume from the outside. Given in the Relativity, space and time in this moving frame have contracted, the inner observers will detect the lessening of volume. But the outer observers, measuring the size of selected region as the whole, detect that the selected space has remained constant. And if the encompassing part remains its size, the encompassed parts in amount do not change their size. Of course, this means only that in the moving frame being inside the selected region, just as the carriers of measures, there have changed only the relative measures that define our perception, not the space as such. “Relative space is some movable dimension or measure of the absolute spaces; which our senses determine by its position to bodies; and which is vulgarly taken for immovable space” [2, p. 30]. It follows from this analysis that relativistic transforms suggest the change of only carriers of measures, and this basically changes the approach to the problem of space-time transform. Should the space transform as whole, we would have to undertake the way of relativists, using the Riemann geometry and giving up the hope to reveal some general properties of space as the whole. But if we suppose only the change of carriers of measures that define our relative perception of space and time, then relativistic hypotheses are excessive, because we deal in this case with the systematic error and may use the trivial metrological solutions to compensate the arising systematic errors. Going this way, we have to redefine some points of basic importance. First of all, the causation in physics points that the contraction of carriers of measures, if it is real, not imaginary, cannot occur as itself but only due to some interaction of material carriers of measures with the environment relative to which these measures move. As we already said, the only possible cause of such interaction can be the change related to the atom field transformation due to motion of atoms relative to the luminiferous medium. But such transformation means the presence of luminiferous aether, so along with the relative reference frames there appears the absolute frame in which the fields of atoms do not transform. With the personification of contraction, the frames lose their equivalence. Or rather, merely kinematically, such relativity can outwardly remain, just as the relativity of acceleration remains merely kinematically. But from the view of dynamics, the relativity fails. If we, after relativists, premise the full equivalence of frames, contraction of measures of one frame with respect to another will be equivalent to the contraction of another frame due to the motion relative to that first. This will simply equalise the measures, as we showed it in previous sections of this work, and we can prove it in general case. For it, we will suppose two mutually moving inertial frames whose parameters are interrelated by one and the same regularity, i.e. if the time interval in unprimed frame is interrelated with related interval in the primed frame as |
| (7.68) |
then |
| (7.69) |
Substituting (7.69) into (7.68), yield |
| (7.70) |
The equality (7.70) can be true only in case if the
function f is inverse to the function g, as “the
function Proceeding from this, |
| (7.71) |
Jointly with the second equality of (7.69), yield |
| (7.72) |
which in the unique fashion defines the unit function. Similarly, we can prove that with the equivalence of frames |
| (7.73) |
Thus, the equivalence of frames causes f and g
to be unit functions, which evidences that there is no transformation of parameters in
both frames. And vice versa, the transformation in the frames can be real only if f
But the non-equivalence as such does not give the solution – to find the correction coefficients that compensate those systematic, as “It is indeed a matter of great difficulty to discover, and effectually to distinguish, the true motion of particular bodies from the apparent; because the parts of that immovable space, in which those motions are performed, do by no means come under the observation of our senses. Yet the thing is not altogether desperate; for we have some arguments to guide us, partly from the apparent motions, which are the differences of the true motions; partly from the forces, which are the causes and effects of the true motion” [2, p. 36]. As we showed in the subsection 6 where we studied the problems of Machian vessel, the possibility shown by Newton how to distinguish the motion “from the forces, which are the causes and effects of the true motion” is applicable to non-inertial frames where these forces reveal themselves. In inertial frames there is applicable Newton’s technique to consider “the apparent motions, which are the differences of the true motions”. In this sense the absolute pattern of transformations of carriers of relative measures can select the absolute frame from the multitude of relative frames. Actually, as we could see in subsection 3, the non-transformed equiphase surfaces reveal themselves only in the frame resting relative to the luminiferous substance. Naturally, the non-transformed field of atom will correspond namely to these non-transformed equiphase surfaces. And, hence, non-transformed parameters of measure of space and time, which we can take as absolute just because relatively to them all moving carriers of measures will be affected by the field transformation, will correspond to them, too. Now let us take an amount of relative frames moving with
different speeds, in premise that we can compare the degree of transformation of the
carriers of measures between any pair of frames. Basing on this comparison, we can build
for n frames the sequence of systematic errors |
| (7.74) |
The only condition for this sequence is, the speeds of all frames comparing with the first frame have to form the sequence |
| (7.75) |
Note that in (7.75) all speeds are more than v12 . This is so because, taking the first point of frame as the initial, we in our relative comparison of speeds automatically establish the chain of inequalities in the increasing order of magnitudes. The chain of inequalities in the decreasing order of magnitudes we will be able to compose only if we attribute a priori some initial speed to the first frame. But in this case also, the further statement will be true, if in the whole sequence the sign of increase either decrease of speeds from the first to last frame remains. Now, to continue the selection of absolute frame, we have to account that the degree of transformation of equiphase surfaces against the speed of frame relative to the luminiferous aether is a monotonous function; hence, in the chain (7.74) two variants can take place: 1) if in the system of inequalities (7.75) the relative speed v12 is zero either non-zero in the frame related to the luminiferous medium, and the sign of v12 is the same as the sign of v1n from the point of absolute frame. In this case the series (7.74) will be, on the whole, a monotonously growing function, i.e., with the growing speed of frame comparing to this first, the systematic error will grow synchronously with the growing degree of transformation of equiphase surfaces of the field; 2) if the sign of v12 is not the same as of v1n from the point of absolute frame, i.e. the frames move in opposite directions relative to the frame of luminiferous substance, the regularity of systematic errors (7.74) will have an extreme. To show it, we have to account that if the first and last frames move oppositely, then in the sequence (7.75), at quite large n we can find some m-th frame that is resting relative to the absolute frame. Its speed for the first frame will be not zero but in its module it will be equal to the speed of first frame relative to that absolute. And this is important, because, if we take some third, k-th, frame, whose relative speed will be |
| (7.76) |
then, as it will move relative to the absolute frame with the same (in module) speed as the first frame but in opposite direction, the systematic error introduced by the carriers of measures comparing with the absolute frame will be same as the error of first frame comparing with the same absolute frame. This last is because of transformation of equiphase surfaces in the absolute frame dependent only on the speed of field source relative to the luminiferous medium but not on the direction of source’s motion. And the equality of systematic errors comparing with the m-th frame means that the measures are equal in the relative measurements between the first and k-th frames. We have to add to this proof that when we considered the monotony of systematic errors, we intentionally stipulated that the sequence has to be true as the whole, because the transformation of fields of atoms can cause the transformation of structure of materials being the carriers of measures. This last can cause definite local anomalies, but in limits of each modification of structure of materials the monotony will be true, the more at small absolute speeds with respect to the luminiferous medium, where we do not expect the modifications. As the second important addition we would like to draw the Reader’s attention that in the derivation, we interrelated as natural the frame in which the systematic errors will be absent and the frame related to the luminiferous aether. Basically, we already have introduced this relationship in the sections 3 and 4, when we showed that both classical and relativistic conceptions equally premise the absolute pattern of transformation of equiphase surfaces of field excitations, which in the unique values interrelates the minimal transformation of these surfaces with the material substance in which these excitations propagate. We also showed that if we substitute the wave processes detected in very many experiments by propagation of some discrete entities, this will give other regularities and properties. Thus, premising the wave nature of field excitations, we automatically premise the presence of quite specific material substance in which these excitations propagate. Summing up the study of relative measurements, we can conclude that it is possible to interrelate the relative and absolute measurements, basing on the absolute properties of some phenomena that reveal in the relative measurements. As we saw, these can be the absolute transformations of carriers of measure either the absolute pattern of forces and accelerations which they cause, but anyway we can establish this interrelation exceptionally through the absolute revelations in relative measurements. And here we will draw especial attention to dynamics, as kinematics which disregards the features of interaction of bodies and fields disables us to distinct the true acceleration from that relative, true motion from imaginary. In particular, “true motion suffers always some change from any force impressed upon the moving body; but relative motion does not necessarily undergo any change by such forces” [2, p. 34]. The same we can state of relative systematic errors: a true systematic of carrier of measure is defined by an absolute motion of the body relative to the luminiferous substance. The relative systematic is defined by the relative motion of frame relative to another frame, and far from always this relative error is real. It can be imaginary (relative in the terms of Newton) if another frame moves, while this studied is absolutely at rest or moves relative to the absolute frame with the less speed that the other frame. “But we may distinguish rest and motion, absolute and relative, one from the other by their properties, causes and effects” [2, p. 32]. As we said above, we can reveal it only after the absolute revelations which just distinguish the absolute motion of body from that relative, as well as “motion and rest, as commonly conceived, are only relatively distinguished; nor are those bodies always truly at rest, which commonly are taken to be so” [2, p. 26]. At the same time, despite exceptional part that absolute measurements take in the measurement evolution, and the main – in generalisation of knowledge of laws of nature, this does not mean at all that the absolute is unreal, abstract, ossified concept. Basically, these are same relative measurements; the only fact distinguishes them that we measure relative to some measures on which the external factors distorting the relative measurements have no effect; but this does not exclude some affection on the absolute measurements. To show it, consider the properties of absolute zero of temperature which we analysed in the subsection 7.2. As we showed there, for the absolute zero of temperature we take the point at which the kinetic energy of molecules and atoms turns to zero and, possibly, only zero oscillations remain. So the theory says; what we have practically? Practically, the kinetic energy of molecules and atoms is known to consist of the energy of chaotic motion relative to each other and of kinetic energy of motion of the studied ensemble of atoms or molecules. Thus, even if the kinetic energy at the absolute zero of temperature reaches zero, but the very frame – e.g., related to the Earth – moves relative to the luminiferous substance, then the general kinetic energy at the absolute zero will achieve only the local minimum whose magnitude will depend on the motion as whole. At small speeds inherent in the Earth’s motion, these corrections will be insignificant. But if speaking of the reference frames moving relative to the absolute frame with the sub-light speed, corrections will be significant and their value will considerably shift the reading point of absolute scale of temperatures. So it appears that even those units of measurements which we take as absolute are, basically, also relative. The difference is only that the systematic errors of absolute measures depend not on the properties of specific carriers of measure but on the pattern of motion of the whole frame as the whole. Due to this, in the frames moving with large speeds, the value of absolute zero will be same irrespectively of the substance with whose help we will find this zero; it will depend only on the pattern, how the frame moves. And this systematic error also will be absolute, as it will turn into zero for the frame resting relative to the luminiferous substance. Similarly with measurement of lengths and time. Having agreed the relative measures with those absolute that rest relative to the luminiferous substance, we yield the reading point relative to which we can find the systematic errors of measurements. But are we sure that in the macro-scale the parts of luminiferous substance do not move relative to the each other? If the substance is material and some processes take place in it, in presence of even insignificant viscosity, in the macro-scale it undoubtedly will cause some mutual displacements and compactions. And these compactions not for certain have to have mechanical nature, it equally can be the redistribution of field strength which we basically cannot measure because of little changes in the regions achievable for our measurements. But it will have an effect on the shift of absolute measures, just as the external factors affect the relative measures. At the same time, even if the global flows of luminiferous substance exist and will be revealed in future, this in no way limits the meaning of absolute measures in our local studies, because “A property, near akin to the preceding, is this, that if a place is moved, whatever is placed therein moves along with it; and therefore a body, which is moved from a place in motion, partakes also of the motion of its place” [2, p. 33]. So, in this case, a local region of luminiferous medium can be thought. Consequently, locally equiphase surfaces will not transform relative to the luminiferous medium – basically, this is just what is needed to attribute to the absolute frame the generality which is necessary to find the systematic errors that arise in relative frames. Noting the said above, we have all grounds to state after Newton that in our local absolute reference frames “ As the order of the parts of time is immutable, so also is the order of the parts of space. Suppose those parts to be moved out of their places, and they will be moved (if the expression may be allowed) out of themselves. For times and spaces are, as it were, the places as well of themselves as of all other things. All things are placed in time as to order of succession; and in space as to order of situation. It is from their essence or nature that they are places; and that the primary places of things should be moveable, is absurd. These are therefore the absolute places; and translations out of those places, are the only absolute motions” [2, p. 32]. With it, in the issues of generalisation of particular experimental studies we may premise that “Absolute, true, and mathematical time, of itself, and from its own nature flows equably without regard to anything external, and by another name is called duration [2, p. 30], “Absolute space, in its own nature, without regard to anything external, remains always similar and immovable” [2, p. 30]. We also may premise that in absolute frames, the space and time are isotropic, premising definite systematic errors taking place in relative frames comparing with the absolute. These errors will be caused exceptionally with the use of material carriers of measures. It is not necessary we to have a direct possibility to compare some body with the absolute frame. Just as in case with the absolute temperature, it is enough to find the transform laws for the carriers of measure in relative frames to get a possibility to introduce the correction coefficients. And here the question arises: which will be the type of frame-to-frame transforms that would help to reveal the regularities of our interest? To find the type of these regularities, we have to join the results yielded above. First of all, proceeding from the properties of time (be it the absolute either relative time), the time transform equations must not include whatever functions of coordinates of frames. As we showed, the presence of such regularities makes the time material. Thus, from the view of ideal transform in which we premise ideal clocks independent of speed of frame relative to the absolute frame, – the time transform will be same as in Galilee transform, i.e. |
| (7.77) |
In parallel, there arises a question, is it possible to transmit the time etalon from the absolute to the relative frame. Here we have to account the fact that such transmission will involve the material carriers whose transformation is unavoidable. So the main task in transmission of absolute measure will be to keep the very absolute measure. With it, disagreement with the relative frame is unavoidable. Thus, for example, if in the absolute calculation we take one second as p periods of radiation of atom in jumping of orbital electrons from one level into another in the absolute frame, then in the relative frame the etalon of one second will be equal to already other number of p' periods of radiation of the same atom. The technique to transmit without deformation we have presented in the supplement to the paper “Notes on physical absolute” [101]. Here we would only mark, this technique is far from being only and we showed it exceptionally to illustrate, this is possible. One more important question touches the efficiency to work with absolute measures in moving frames. In full accordance with Newton, if we use the results of measurements, doing not exceeding the limits of our own frame and doing not generalising these results out of this frame, the relative measures give us no trouble, just so as still were satisfying the relative measures based on the parts of human body or on sand flowing from one vessel to another. We also need not the absolute measures when we are interested not in the very absolute values but their interrelations based on same etalons in the same frame. But if we want to generalise the results of measurements for other frames, if we are interested in general regularities and interrelation of processes, we have to operate with measures common for different frames and for different conditions of measurement. Relative measures will give some distortions which we will be unable to reveal until we reduce the relative measures to those absolute. Just so “Absolute time, in astronomy, is distinguished from relative, by the equation or correlation of the vulgar time. For the natural days are truly unequal, though they are commonly considered as equal and used for a measure of time; astronomers correct this inequality for their more accurate deducing of the celestial motions. It may be, that there is no such thing as an equable motion, whereby time may be accurately measured. All motions may be accelerated and retarded, but the true, or equable, progress of absolute time is liable to no change. The duration or perseverance of the existence of things remains the same, whether the motions are swift or slow, or none at all: and therefore, it ought to be distinguished from what are only sensible measures thereof; and out of which we collect it, by means of the astronomical equation. The necessity of which equation, for determining the times of a phenomenon, is evinced as well from the experiments of the pendulum clock, as by eclipses of the satellites of Jupiter” [2, p. 31–32]. And though this technique can seem too complicated, just it allows to select the real processes and motions, not distorted by the carriers of measures. Thus, if we deal with study of general regularities, the Galilean time transforms remain and we study the behaviour of material bodies, fields, time processes in the light of affection of external factors to which we would attribute the type of motion of the accompanying frame. If the transforms are true with account of real construction of clocks, we have to introduce the correction coefficient. And in case of transform from one space homogeneous in the pace of time to another, also relative space, the coefficient can depend only on the mutual speed and can be individual for each kind of clock mechanisms, i.e. |
| (7.78) |
In case of passing from the space inhomogeneous in the pace of time to another space, also inhomogeneous in the pace of time, the matching coefficient will depend also on the location of checked clocks in both frames, i.e. |
| (7.79) |
where xA , yA , zA and x'B' , y'B' , z'B' relatively are locations of particular clocks in both frames. The coefficient kt has to be individual for each kind of clocks; the dependence on the location of clocks has to include the particular location of both clocks and cannot be considered as a function of spatial coordinates in the frame-to-frame transforms. These limitations are introduced because the inhomogeneity of pace of relative time in some frame must not lead us to the materialisation of time, as it happened in Relativity. To keep the basic properties of time and the plane of events is the main stipulation when we form transforms physically correctly. Concerning the spatial transforms, we also have to differ the ideal and real transforms, as well as the transforms for material points and for wave processes. For ideal transforms, the Galilean transforms fully remain true, as well as the features which we described for the measurement of absolute time, as we disregard the transformations of carriers of measure of length, given the change of carriers of length does not reflect on the space as the whole but only changes our local perception of environment. So, if we join two processes – the transformation of properties of studied phenomenon and of measures with whose help we study it – we only will complicate the generalisation of processes and phenomena. The technique to transmit the measures of length without distortion also has been considered in our previous paper “On longitudinal excitation of elastic medium having a moving boundary” [102, p. 20]. For material points, if we transform from a homogeneous relative space into another homogeneous relative space, using the relative measures, general laws will be very similar to those Galilean; namely, |
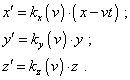 |
(7.80) |
With it, just as in case of time transform, we have to distinguish the ideal and real transformation. For homogeneous spaces, in supposition of ideal measures of length, it would be perhaps most useful to use the degree of transformation of equiphase surfaces – namely, with enough accuracy we can take the diameter of equiphase surface for the same moment of time in the compared frames after it was radiated by the source. In transformation of real relative measures applied on a material carrier, we have to account the properties of material of carrier. For wave processes, the transform laws will be basically same, but we have to additionally account the properties of wave processes considered in the section 3 and, in particular, that the equiphase surfaces have the absolute pattern of transformation. It is also important to account in calculations that the relative speed from the point of frames moving differently relative to the absolute frame will be measured differently, on the whole. So, to transform correctly, it would be best to use as the basic the absolute frame and the frame relative to it, to define all mutual characteristics. Of course, the described transforms are not so much elegant as we would expect, but the laws of transform of measures in the frames moving with the sub-light speeds also are not simple and depend on many factors which are reduced, if speaking generally, to the complicated deformation of fields. In that number, it is not worthy to exclude that in these frames some laws of dynamics can be untrue. This adds the importance to the absolute frame whose use allows to apply the Newton laws of dynamics to the processes going in the frames moving with large speeds. In this case we can gain the convenience from the fact that, using the absolute frame, we study not the laws of transform of the carriers of measure but the laws of transform of the bodies and phenomena themselves. While it is not difficult to translate the regularities from absolute to relative units, if the previously revealed regularities are available. Proceeding from the said, if we approach to the relative and absolute frames with a correct account of affecting factors, not proceeding from simplicity and elegance, we can expect to get over the paradoxes and discrepancies that take place in the existing conceptions. |
Contents: / 53 / 54 / 55 / 56 / 57 / 58 / 59 / 60 / 61 / 62 / 63 / 64 / 65 / 66 / 67 / 68 / 69 / 70 / 71 / 72 / 73 / 74 / 75 / 76 / 77 / 78 / 79 / 80 / 81 / 82 / 83 /