SELF |
80 |
S.B. Karavashkin and O.N. Karavashkina |
|
|
|
SELF |
80 |
S.B. Karavashkin and O.N. Karavashkina |
|
|
|
7.1.5. Correctness of speed composition in the relativistic mechanics Having proven that the relativistic time transform is incorrect, we proved also the incorrectness of postulational basis based on the hypothesis of constant lightspeed in all inertial frames. But we still have unanswered a question of interrelation between the mutual speed of bodies A and F relative to the frame S on one hand and speed of A relative to F calculated through some intermediate frame S'' – on the other. And though this issue cannot influence the proof that the time transform is absent in mutually moving frames, we will consider this aspect, lest to leave unproven statements. Consider the motion of some body F with the speed u in direction of positive axis x of some resting inertial frame S in whose origin we have some body A resting in this frame, as is shown in Fig. 7.4.
|
Fig. 7.4. The motion of a body F relative to the resting frame S
|
According to practice, we can measure the speed of this body motion in different ways – both directly and through any intermediate frame. Anyway we have to yield same result, as it says the parallelogram law of velocities composition (generally). But Einstein, following the principle “if there is a discrepancy between his abstract statements and practice, this is worse for practice”, – said “that the speed parallelogram law that made us thinking impossible to agree the Lorentz theory with the principle of relativity is based on arbitrary and inadmissible hypotheses. Actually, this law leads to the following transform formulas: |
| (7.51) |
or, in more general appearance, |
| (7.52) |
As we saw, the first of these relationships expresses a poorly grounded hypothesis of time coordinates of elementary event taken with respect to two reference frames S and S' moving uniformly and rectilinearly to each other. The rest three relationships express the hypothesis that the kinematic configuration of frame S' relative to the frame S is identical to the geometrical configuration of the frame S' ” [17, p. 151]. Above we already considered the issue related to the so-called ‘poorly grounded hypothesis’ that the time transformation is absent and showed that not classical physics is based on poorly grounded hypotheses but just Relativity, basing on fully ungrounded hypothesis of constant lightspeed in any inertial frames, has built a self-contradictory, we even can say – absurd pattern of transformation processes and non-simultaneity of events. And as concerns the kinematic configuration, we can point that, violating the parallelogram law in mechanics, relativists agree that the speed of an object measured by several independent techniques will be different. This subsection we will render to analyse, how much legal are such statements of relativists. To make a full consideration, let us first see, how relativists themselves substantiate the speeds composition. Consider the equation of motion of a point moving relative to S' uniformly with the speed u: |
| (7.53) |
If, using the relationships (I) (trivial Lorentz transforms – Authors) we instead x', y', z', t' substitute to them their expressions through x, y, z, t , we will yield x, y, z as the functions of t and, consequently, the components ux , uy , uz of the speed u of the point relative to the frame S. Thus, we can yield the formula that will express the speeds composition theorem in its general appearance, and then it will be immediately clear that the parallelogram law is applicable only as the first approximation. In the particular case, when the speed u' has the same direction as the speed v of forward motion of S' relative to S, we can easily yield that |
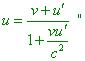 |
(7.54) |
[17, p. 156 – 157]. We see from the citation: the speeds in Relativity are composed so that the speed v of intermediate frame is measured with respect to the resting frame, and the speed u' is measured from the intermediate frame. While we find the speed u in (7.54) as the real speed of material point relative to the resting frame, which is important for the further analysis. And if the intermediate frame moves relative to that resting with the speed v, the resting frame moves relative to that intermediate with the same speed in the reverse direction. The same we can say about the speed u' . But we cannot say that in SRT the speed u' will be such from the point of resting frame. Though it seems, speeds v and u' are measured from one intermediate frame – which means, by the same measures – and if the mutual speed of the resting and moving frames is same, the speed u' also has to be same from the point of resting frame. But in this case in SRT just the asymmetry of transform of which we spoke in the section 4 comes into force. Just due to the asymmetry these speeds will be transformed differently. In SRT, only the between-frames speeds are transformed without transformation. So further we will account this feature that, basically, is unable to prevent our study, but it needs to be accounted. Returning now to our Fig. 7.4, introduce to its scheme the third frame S'' whose speed relative to the frame S we will take as v, and relative to the frame S' – as (V - v) . Should we analysed in classical formalism, it would automatically follow from these additional definitions in Fig. 7.4 that from the point of S'' , the mutual speed of bodies A and F would be |
| (7.55) |
Similarly, the speed of body F from the point of S – and, hence, of the body A, too – would be |
| (7.56) |
Conjunction of solutions yielded in two different ways of measurement makes the discrepancies and paradoxes absent. Another situation is in SRT. From the introduced additional definitions we can only say that the speed of virtual frame S'' relative to S is v, and the speed of body F, and with it also the speed of frame S' relative S'' is (V - v) . We also can say that the speed v can be thought in limits |
| (7.57) |
and take any value of this range. The speed V also can be thought in limits |
| (7.58) |
where c is the lightspeed. Basing on the available data, we can apply the Einsteinian formula for speeds composition (7.54). The resulting speed of the body F relative to A measured through the intermediate frame will be determined as |
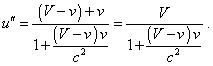 |
(7.59) |
As follows from it, which speed of intermediate frame will we take, such will be the measured speed of body F relative to A. At the same time, as we solve the problem in general form, we may attribute to the intermediate frame an arbitrary speed in the limits (7.57). Moreover, we may introduce few such virtual frames with different speeds. So for each case we will yield its own value of speed between F and A. But undoubtedly, the speed between F and A is unique-valued, it cannot depend on the virtual frames which we introduced; this points us that relativistic composition of speeds is incorrect. We can determine this value of speed immediately from (7.59), setting to zero the speed of intermediate frame, as in this case the frame becomes resting relative to the frame connected with the body A. For this case we yield |
| (7.60) |
The same result we will yield in coincidence of the speed of intermediate frame with that of body F. Thus we see, the mutual speed of bodies F and A measured from the intermediate frame is equal to the speed between these bodies measured from any frame related to one of these bodies. This fully corroborates that the parallelogram of speeds remains and that SRT illegally deforms the pattern of processes. We should add, the relativistic parallelogram law does not agree with requirements of the very Relativity. Actually, if we plot u(v) for different V, using the limits of measurements (7.57) and (7.58), we will yield the curves shown in Fig. 7.5.
|
Fig. 7.5. The plot u(v) for different V
|
In this figure we first of all see that with the positive v, the speed between F and A can take any values, including the lightspeed, and this property remains at small values of V. Thus, Einstein might not state that at small speeds of motions of real bodies, relativistic mechanics is reduced to that classical. Choosing the speed of virtual intermediate frame close to the lightspeed, we at small speeds between the bodies will yield in Relativity the same indefiniteness. But the main feature of the plot reveals itself at negative values of v, when the intermediate frame moves oppositely to the motion of F relative to A. In this case the plot shows divergence, and despite speeds v and V remain in limits allowed by Relativity, the resulting speed can take any values, up to infinite. Einstein did not notice this feature, as he limited his
consideration by the case when v and V coincide in directions (i.e. by the
positive values of v): “From this relationship (the
formula (7.54) – Authors)
we see that in composition of two speeds less than the lightspeed in the void, the
resulting speed is always less than the lightspeed. Actually, if we take v = c
- |
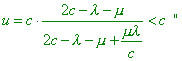 |
(7.61) |
[17, p. 157]. In reality, we may not limit the direction of speeds and have to account both positive and negative their values. But we see that in composition of speeds less than the lightspeed, in Relativity the motion faster than lightspeed is possible. And this motion is the same virtual as virtual is the very intermediate frame through which we calculate the speed of F relative to A. Relativists can argue here: the situation when the total speed of body’s motion is faster than light is impossible, as one of observers cannot fully detect the location and pattern of motion of the rest parts of the model. So in Fig. 7.6 we show the particular scheme in which all observers in all frames can observe other frames, v and V will be less than the lightspeed, but the relativistic speed of motion of body F relative to A will exceed the lightspeed.
|
Fig. 7.6. The motion of frames with the negative value of the speed v. All observers in this scheme will see each other, and the total relativistic speed of F relative to A will be inverse and faster than the lightspeed
|
The mutual observability in Fig. 7.6 is provided by the fact that the frame S'' moves towards the frame of body F. Thereupon, all light signals reach the measured objects. If now we calculate the speed u'' in accordance with (7.59), we will yield |
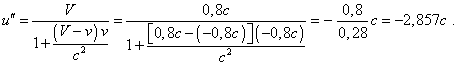 |
(7.62) |
This result corroborates that the faster-than-light speed can be achieved in Relativity, and inversely to the motion of body F relative to A, while the real speed of the body F relative to A is u = V = 0,8 c . In Fig. 7.5 the negative value of resulting speed u'' can be shown in real models in the counter motion of studied body F and intermediate frame S'' . Again, suppose that because of indefinite result of mediated finding of the speed between bodies, it is legal to calculate this speed only immediately within the relativistic formalism. Then, due to this prohibition, the relativistic formulas describing the Doppler effect become illegitimate, because they both have been derived on the basis of relativistic law of velocities composition. Thus, we see that violation of the parallelogram law unavoidably leads to the inner discrepancies, and the main, to the indefiniteness in finding of speed, when, taking some arbitrary virtual frame, we can yield any value of speed between bodies, even if factually this speed is so little that we can measure it non-relativistically. This corroborates again the incorrectness of relativistic approach to the problem of space-time based on non-physical statement that the lightspeed is constant in all inertial reference frames, – just the statement from which there immediately follows the absurd transformation of space-time and ungrounded violation of the law of velocities composition. This is a natural result for physics; it shows again how incorrect is it to substitute the phenomenology by mere formulas yielded in manipulations with symbols that have been cut off the features of physical processes. |
Contents: / 53 / 54 / 55 / 56 / 57 / 58 / 59 / 60 / 61 / 62 / 63 / 64 / 65 / 66 / 67 / 68 / 69 / 70 / 71 / 72 / 73 / 74 / 75 / 76 / 77 / 78 / 79 / 80 / 81 / 82 / 83 /