SELF |
68 |
S.B. Karavashkin and O.N. Karavashkina |
|
|
|
SELF |
68 |
S.B. Karavashkin and O.N. Karavashkina |
|
|
|
6.4. The features of inertia forces affection in accelerated motion of the body To answer this part of question, we have, additionally to the factors accounted above (which reveal the causation between the affection of external force and producing of the force of inertia) to account the features of affection of the force as such, first of all the important circumstance that “one of the most important characteristics of the force is its material origin” [63, p. 210]. In the most general classification, “we can classify the forces affecting a solid body as external and internal. Forces affecting the particles of this body from the side of other material bodies are called external. Forces by which the particles of this body affect each other are called internal. The force applied to the body at some its point is called lumped. Forces affecting all points of the given volume or of the given part of body’s surface are called distributed. … In particular, the force of gravity affecting the given solid body that usually is considered in mechanics, is the resultant of the gravity force of its particles” [64, p. 18]. Basing on this classification, consider the features of lumped and distributed (or usually called also spatial) forces. Let us begin with lumped forces that have a direct relation to the origin of centrifugal forces in the revolving vessel with water. 6.4.1. The features of revelation of inertia forces under affection of lumped forces As it follows from the above definition, if the studied body is strongly constrained with the revolution axis at some its own point, the forces providing the affection on the body are lumped, as this constraint is connected to a particular physical point or to a small part of body’s surface. With it all other parts of the body remain together with the points of contact with constraints, by forces of coalescence within the body, i.e. by the inner forces or, as they are also called, elasticity forces. So it appears that in case of lumped forces, there in revolution take part both exterior and interior forces due to which the affection propagates from the point of constraint to other parts of the body. We can visualise this affection, drawing the interior forces as springs, see Fig. 6.5. |
Fig. 6.5. Scheme describing how the centrifugal and centripetal forces arise in case when affection is applied to the start point of the chain of equal masses
|
We can easily calculate this scheme by the technique of recurrence; true, with it, the larger number of calculated masses the more complicated expressions are. So let us confine ourselves to four masses, that will be enough to find the regularity without limitation of generality. Let the initial location of masses before revolution be such that all distances between them are equal, i.e. in case of our four masses |
| (6.18) |
We should point that in revolution, the distances between all masses are not equal, as (6.18) predicts, so we have to introduce additional changes of the initial condition in order to determine the pattern of mass redistribution. Let us do it so: |
| (6.19) |
With it, conveniently introduce the intermediate parameter ri : |
| (6.20) |
Also conveniently, begin solving from the last, fourth mass. As only the elasticity of spring provides its revolution, with account of regularity of centrifugal and centripetal forces we can write |
| (6.21) |
where |
| (6.22) |
from where |
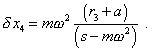 |
(6.23) |
It follows from (6.23) that the transformation of spring
curving the trajectory of the last body depends both on stiffness of spring and on the
frequency of revolution of the elastic chain. It also follows from (6.23) that We can determine r3 , modelling the conditions of motion for the third body. Already two springs affect it, so the equations of forces for this body will be |
| (6.24) |
Substituting |
| (6.25) |
Accounting (6.19) and (6.20) again, yield |
| (6.26) |
Solving with respect to |
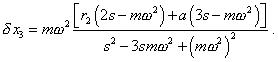 |
(6.27) |
We see from (6.27) that the change in the third spring
also depends on the revolution frequency and on the location of previous, second mass, but
the relationship is well more complicated than for Going same way, consider the balance of forces for the second mass. The modelling equation will be |
| (6.28) |
After the transforms yield |
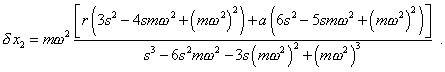 |
(6.29) |
We see from (6.29) that
|
Fig. 6.6. Distribution of masses (blue markers) of an
elastic chain in its stable revolution about the resting centre, with the rigid constraint
connected to the first mass; the initial location of masses is shown by lilac markers. The
parameters of scheme: r = 1 m; a = 0,1 m; m
= 0,1 kg; s = 100 N/m;
|
In Fig. 6.6. we see the expected decrease of the tension of springs when closer to the end of chain. This evidences that the value of centripetal force depends not only on the mass to which it is applied but also on the interrelation of this mass with the next masses. The longer chain the stronger influence, and it depends on the parameters of elastic chain and on the frequency of revolution. This dependence of relative transformations of initial between-masses intervals on the relative radius of revolution of masses is shown in Fig. 6.7.
|
Fig. 6.7. Dependence of relative transformation of initial between-masses intervals on the relative radius of revolution of masses at different frequencies of revolution
|
Mach with his idea of influence of surrounding gravity masses was unable to yield such regularities, of course. All what he could model, basing on the premise of universal nature of centrifugal forces, was fully indefinite: “… only limited number of masses is accessible for our study, so we cannot finish this summation. … It remains only to wait until we have this experience” [61, p. 59]. Thus, having quitted a clear regularity described by Newton, Mach came to the same indefiniteness which then allowed relativists to revise the physical laws without care, how much it corresponds to the physical processes. In this light, we should not expect to be in progress with our experimental knowledge, as Mach’s premise that his definition of inertia “… gives the same as usual, as far as there exists enough bodies in the world space that seem to be at rest” [61, p. 59] is incorrect in its very statement, as it is based on the outwardly seemed, not on the process comprehensively stipulated in the amount of revealed properties. “Should I be able whenever meet this philosopher which seems to me to be well higher than many other followers of this theory, to show him my good will, I would recall him the phenomenon which he surely saw thousand times and from which we can understand, in full accordance with what we said, how easily can we be deceived by a simple appearance or, say, image of feeling. This phenomenon is the following. People going in the night street have an impression as if the moon goes with the same pace as they do, when they see it sliding along the drain gutters on roofs above which it appears just as a cat which actually, going the roof, would follow them. This appearance would too obviously deceive the vision, should the mind intervene” [39, p. 193]. |
Contents: / 53 / 54 / 55 / 56 / 57 / 58 / 59 / 60 / 61 / 62 / 63 / 64 / 65 / 66 / 67 / 68 / 69 / 70 / 71 / 72 / 73 / 74 / 75 / 76 / 77 / 78 / 79 / 80 / 81 / 82 / 83 /