V.6 No 1 |
69 |
| The problem of physical time in today physics | |
|
|
V.6 No 1 |
69 |
| The problem of physical time in today physics | |
|
|
We can conform the many-sided revelation of same regularities that Newton differed in his definitions of ‘pressure’ and ‘resistance’ and mark, our solution is not the only. If we anchor not first but last mass, we will yield not tension but shrinkage of between-mass springs, and it still will be in full agreement with Newton in the meaning that masses will always tend to take the utmost distance from the centre of revolution. To show it, let us calculate the scheme in which the rigid constraint is anchored to the last, fourth mass (see Fig. 6.8).
|
Fig. 6.8. The scheme describing how centrifugal and centripetal forces arise in case when the end of elastic chain of equal masses is affected
|
To solve this problem, we can make use of same initial conditions and with same recurrence (with some changed symbols) will seek the solution, only now we will begin with the first mass and gradually move to the point where the rigid constraint is anchored. To write the modelling equation for the first mass, we have to account that in this case the elasticity of spring will compensate the centrifugal force because of shrinkage, so the first equation will be |
| (6.30) |
From (6.30) we yield |
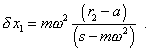 |
(6.31) |
Comparing (6.31) with (6.23), we see that the difference in solutions is that the sign plus is substituted for minus in the multiplier of numerator. It just says us that in the first problem, when the start of chain was anchored, revolution caused the lengthening of spring, and when the end of chain was anchored, revolution caused its shrinkage. Below we will show that the observer can easily detect these deformations directly in the revolving frame. Going along the chain, we will sequentially yield |
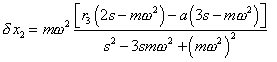 |
(6.32) |
and |
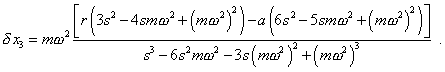 |
(6.33) |
The typical mass distribution along the elastic chain yielded in this calculation is shown in Fig. 6.9.
|
Fig. 6.9. The mass distribution (blue markers) of an
elastic chain revolving about resting centre on a rigid constraint connected to the fourth
mass. The initial location of masses is shown by the lilac markers. The parameters of
scheme: r = 1 m; a = 0,1 m; m = 0,1 kg; s
= 100 N/m;
|
We see that, as opposite to the previous problem, the stationary state of elastic system is provided by the spring compression and the spring most far from the anchored point experiences the minimal transformation, while the utmost transformations are in the spring nearest to the anchored mass. From this, a break in the elastic chain in both cases will occur just at the point of anchor, and this property will be true for any material bodies involved into revolution, as all material bodies are elastic and can be modelled by an elastic chain. But from the view of our study, the most important is the difference in the degree of bodies’ transformation in the radius from the centre of revolution. On this basis we already may not speak of identity of absolute and relative accelerations, as relativists insist: “… a simple analysis shows that we may assume the acceleration only as the acceleration relative to other bodies, i.e. that we are able to determine it only as a relative acceleration. So it is doubtful that the law of motion by Galilee – Newton, which states that the bodies resist the acceleration, contains some statements about acceleration as such (i.e., about absolute, not relative acceleration). The new theory is free of this inconsistency; the inertia reveals itself in it as the resistance to the relative acceleration of bodies” [65, p. 318]. We see from calculation that the pattern of transformation of chain depends on the frequency of revolution, on elasticity of springs, on masses and on the way, how the constraint is connected. If the chain was unfastened and the constraint revolved relative to the chain that lays apart, deformation surely cannot arise in the spring – and this distinguishes the relative acceleration from that absolute. And though mere kinematically we would be able to draw the trajectories of this spring from the revolving frame and yield the imaginary acceleration of the elastic chain, anyway, the revolving body will gain acceleration, not the body which is not involved in the revolution, just as mechanics is not limited by the laws of kinematics. The more, if we approach the issue of equivalence of inertial and non-inertial frames exceptionally from the kinematic view, as relativists do: “the kinematic equivalence of two coordinate systems factually is not limited by the case when both frames K and K' move relative to each other uniformly and forwardly. From the kinematic view, this equivalence the same well works, for example, if one frame orbits about another one” [54, p. 327], – we have first of all to account that in kinematics the concept of inertia forces does not exist, this is the term of dynamics. Relativists, relying on the outward kinematic likeness, try to generalise not the laws of kinematics but just the laws of dynamics, in this way violating the inner consistence of physical laws: “may we conclude from it that the frame K' is (absolutely) accelerated? This conclusion would be illegal. We can equally think the frame K' ‘resting’, premising only that in the frame K' there exists a homogeneous gravity field that is the cause of accelerated motion of the bodies relative to K' ” [45, p. 422]. If we confine ourselves to the kinematic characteristics, Newton wrote of this case in his “Principia” so: “For all the parts of revolving bodies endeavour to recede from the axis of motion; and the impetus of bodies moving forward, arises from the joint impetus of all the parts. Therefore, if surrounding bodies are moved, those that are relatively at rest within them, will partake of their motion. Upon which account, the true and absolute motion of a body cannot be determined by the translation of it from those which only seem to rest” [2, p. 33]. At the same time the kinematic likeness disables us to introduce into consideration any forces, as “kinematics is a part of mechanics that studies the geometric properties of bodies’ motion, disregarding their inertia (mass) and forces affecting them” [64, p. 138]. “… The true and absolute motion of a body cannot be determined by the translation of it from those which only seem to rest”, and in order to find this motion, we have to make sure that “the external bodies ought not only to appear at rest, but to be really at rest” [2, p. 33], as “The causes by which true and relative motions are distinguished, one from the other, are the forces impressed upon bodies to generate motion” [2, p. 33]. And these problems are already solved in the formalism of dynamics. With it, we cannot say that dynamics has an effect only on the laws of dynamics itself. Because of dynamic transformations, the mutual arrangement of parts of a body changes; this means, the configuration of model changes, too. Due to this, the trajectories of motion of separate parts of model, and in some cases of model as the whole, change. And if sometimes we do not see this change of configuration and trajectory, this does not mean that we may ignore the influence of laws of dynamics and confine ourselves to the laws of kinematics, as these last, being limited, are unable to account the change of configuration or trajectory that follow from the dynamic transformations. “Thus, it would be better to leave the appearance concerning which we all agree and to try through reasoning either to corroborate the reality of premise or to unmask its delusiveness” [39, p. 192]. Also, it is senseless to speak in frames of mechanics that we prefer or do not prefer inertial frames. As we showed in the sections 3 and 4 of our study, all properties that determine the absolute frame, as well as the property of isotropy of the light speed in relation to the absolute frame, reveal themselves as the consequence of interaction of the wave excitation with the luminiferous substance. While in kinematics we consider exceptionally processes of motion, doing not clearing the physical causes producing them, and if we account the exterior and interior forces, the references to the kinematic likeness are incorrect. In limits of dynamics, we can simply and obviously identify the absolute acceleration that arises under affection of lumped forces. If we, for example, place two or more elastic chains with different stiffness coefficients anchored on a common constraint, as we show it in Fig. 6.10, we can reveal through the difference in the degree of transformation that the frame revolves, and this technique is applicable both to revolution and to the linear acceleration/deceleration under affection of lumped forces.
|
Fig. 6.10. Transformation of three elastic chains having different stiffness coefficients. They have a common constraint and revolve with same frequency; the parameters of chains are r = 1 m; a = 0,1 m; m = 0,1 kg
|
Fig. 6.10 also shows that if the elastic chain does not revolve (the upper chain), its length will differ from the lengths of chains that participate in the revolution. This proves that inertia reveals itself just when the body is affected by a force, and affection reveals just in the change of trajectories of chain elements motion. Developing this conclusion, we can use Fig. 6.10 to find the accelerated motion in the rectilinear acceleration of the body; with it we will yield the alike pattern of different transformation of chains, dependently on the elasticity of constraints. With it, the transformations will be always directed against the applied force. This corroborates Newton’s conclusions that the inertia force is always the force of resistance of a body to the change of state of its motion and remains such, irrespectively of, whether the affecting external force changes the speed or the direction of its motion. Consequently, in case when the revolution arises under affection of lumped forces, we may not identify the frame related to the revolving body with the inertial frame, and the accelerated pattern of motion can be clearly revealed within the revolving frame. |
Contents: / 53 / 54 / 55 / 56 / 57 / 58 / 59 / 60 / 61 / 62 / 63 / 64 / 65 / 66 / 67 / 68 / 69 / 70 / 71 / 72 / 73 / 74 / 75 / 76 / 77 / 78 / 79 / 80 / 81 / 82 / 83 /