V.6 No 1 |
57 |
| The problem of physical time in today physics | |
|
|
V.6 No 1 |
57 |
| The problem of physical time in today physics | |
|
|
To see the cause of this difference, determine the speeds of wave propagation for the first and second approaches to this problem. It will be sufficient to take derivatives in time of the systems (3.3) and (3.8) respectively. In the case of moving frame yield |
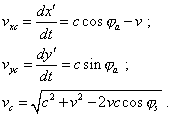 |
(3.13) |
In the case of moving source yield |
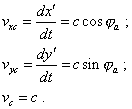 |
(3.14) |
Thus we see, if the frame moved with respect to source, the speed of light in the moving frame varies from c + v to c - v , and in the second case, when the source moved with respect to the frame, the speed of light is isotropic and equal to c. This is because the frame rests with respect to medium in which the wave processes propagate. It appears that when we did the transformation from one frame to another, premising the isotropic propagation of light in the resting frame, we silently premised that the resting frame relates to the medium in which the light waves propagate. But when we considered processes immediately in the moving frame taking it as the resting, then despite our additional claims of its motion, it became resting by the meaning which we gave it – with respect to the luminiferous medium, irrespectively of our additional claims. This duality raises a question: should we account some additional features of the frame, could we yield the results of first modelling in limits of second? It appears, we could not, as the difference arises just when we rise the question, whether the frame moves with respect to the luminiferous medium. Answering this question, we have to remember of this medium, to interrelate the frame with it, to determine the speed of moving frame and of the source with respect to this medium and only after it we may solve the problem in the moving frame. The very fact of source’s motion in relation to the given frame does not evidence that the source is at rest with respect to the aether. If both the frame and source move with some speeds with respect to the luminiferous medium, the solution will depend on this co-motion. To show it, premise that the source moves with respect to the luminiferous medium with the speed vs with the positive direction of the axis x of the frame related to this medium. The second inertial frame moves in the same direction with the speed vr . We should immediately draw our attention: as opposite to previous models, the frame and source move in positive direction. We made this change to provide the common approach, supposing that the speed of frame can be both positive and negative. In this way we on one hand generalise our model, and on the other keep the possibility to compare our results with the models studied before. To plot the pattern, how the equiphase surfaces propagate in the moving frame, we have to apply sequentially the results of previous particular models. Let us first determine the shape of some arbitrarily chosen equiphase surface in relation to the resting frame. According to (3.8), noting the signs, its equation will be |
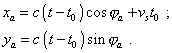 |
(3.15) |
Now, knowing the pattern of equiphase surfaces in the resting frame, let us pass to the moving frame, applying the transformation (3.2). Yield |
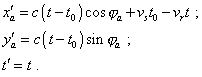 |
(3.16) |
As we expected, this solution is the superposition of two above models. The dynamic diagram plotted with (3.16) is shown in Fig. 3.4.
|
Fig. 3.4. Dynamic diagram of light equiphase surfaces propagation when the moving source and moving frame with the speeds vs = - 0,8 c and vr = - 0,6 c relatively, for the moments of time from t0 = 0 to t0 = 6T , where t0 is the moment of radiation of the equiphase surface; the world line of the observer is denoted in blue
|
We see from the construction that the pattern of transformation of equiphase surfaces did not change comparing with Fig. 3.2 which, as we revealed, was calculated from the point of frame resting with respect to the luminiferous medium. Only the inclination of the source’s world line has changed. Hence, the transformation of equiphase surfaces is absolute and independent of the frame. At the same time it does not mean that the observer in the moving frame will yield unchanged characteristics of the light signal irrespectively of the speed of its frame with respect to the luminiferous medium. To show it, determine the propagation speed of equiphase surface from the point of observer in the moving frame. Use the above technique and differentiate the system (3.16) in time. We will yield in full accordance with (3.13) |
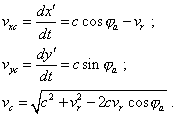 |
(3.17) |
This expression corroborates again that, when we took the moving frame as resting, then, taking vr = 0 , we made it resting not only with respect to the observer but with respect to the luminiferous medium, so we automatically yielded the isotropic propagation of light, in accordance with (3.14) and (3.17). Now determine the regularity of transformation of the period between the equiphase surfaces from the point of moving observer. Noting the above technique, suppose that the source radiates the equiphase surface at some moment t0 and the observer detects it at the point x'1 of the moving frame at the moment t1 . Then, in accordance with (3.16), |
| (3.18) |
Suppose that the next pulse radiated by the source at t0 + T the observer detects at t1 + T ' at the same point of the moving frame. For this next pulse yield |
| (3.19) |
Subtracting (3.18) from (3.19), with a simple transformation, yield |
| (3.20) |
The yielded expression (3.20) corroborates that we may not think the motion of frame and motion of source as interchangeable, as their values are in (3.20) asymmetrical. Should the speeds of frame were involved in (3.20) as their difference either sum, we could speak of equivalence of approaches, and only in case of particular measurements, as generally, as we could see above, the luminiferous medium has a high effect on the pattern of equiphase surfaces propagation. At the same time, we see from (3.20) that irrespectively of the speed of motion of the source and frame, at synchronous speeds the periods of radiation and reception of the light pulses are equal. This means, irrespectively of the degree of transformation of the equiphase surfaces, if the source and observer are mutually resting, any atomic clock will read same time intervals, but in no case in accordance with the relativistic prediction: “the observed slower pace of other clocks is predicted, according to the Lorentz transforms, for the clocks of all three types – number, mass and volume, if only each of them measure the time variable … in their reference system” [24, p. 153]. Summing up the study of equivalence of the way to pass from one inertial frame to another, we can conclude that the description of the field processes to which the light propagation relates is non-equivalent in different frames, as the luminiferous medium affects the studied processes. And if in the beginning of our consideration we were sure that nothing prevents us, instead the immediate transformation from one frame to another, to consider just the processes in the moving frame, now, with the made analysis, we can state such substitution inadmissible. Taking the moving frame as resting, we automatically make it resting with respect to the luminiferous medium in which the wave processes propagate. Due to this, the frame related to the substance in which the wave processes propagate becomes selected. Just in it the light speed is isotropic. In all other frames the light speed is inconstant and varies dependently on the direction and speed of frame’s motion in relation to the medium, i.e., to the resting frame which really gains the properties of the absolute reference frame. We also saw that far from always in the particular studies we are able to reveal the true meaning of processes; this adds importance to Newton’s statement of the necessity to account the relative kind of measurements when we perceive the processes and build the generalised models. Though, on the other hand, our study showed the formalism of classical physics able to account the field processes namely at the level of generalisation showing the difference between the frame equivalence in studying the processes of motion of material points and non-equivalence of these frames in studying the field propagation in space and time. This conclusion shows illegal, of course, this basis thought of Einstein: “The special theory of relativity is based on the following postulate being true also for the Galilee – Newton mechanics. If we chose the coordinate system K so that the physical laws in it are true in its simplest form, the same laws are true in every coordinate system K' that moves uniformly and directly with respect to K” [25, p. 453]. The initial mistake was, having passed to the area of wave processes determining the propagation of light waves, relativists did not think of the changes that will take place in such passing, though, as we could see, these changes are very simple for understanding and calculation. Moreover, as we marked in the introduction, relativists went even farther and separated the particular mathematical expressions based on the equivalence of frames for the material points from the physics of processes, so they lost the possibility to really account the features of modelling of the field processes. Just so the whole relativistic conception from the very beginning was based on the non-associative admissions and distortions like this: “Thus, the previous way of a definite construction of the coordinate system in the space-time continuum appears inapplicable; it seems that there is no way that would make possible to adjust to the 4-D world such coordinate systems with whose help we could expect to formulate the laws of nature in a simplest way. So it remains nothing but to admit all thinkable coordinate systems basically equal to describe the nature. This is the same as to require: General laws of nature have to be expressed through the equations that are true in all coordinate systems, i.e. these equations have to be covariant with respect to any substitutions (commonly covariant). The physics satisfying this postulate will obviously satisfy the general postulate of relativity, as the amount of all substitutions will anyway incorporate those which correspond to all relative motions of (3-D) coordinate systems. As this requirement of common covariance that takes from the space and time its last physical objectivity (! – Authors) is natural, it will be seen from the following consideration. All our space-time ascertaining is always reduced to establish the space-time coincidence. If, for example, the events be only the motion of material points, we would finally observe only meetings of two or several such points. The results of our measurements are also nothing else as detection of such meetings of material points of our scale with other material points, and relatively of coincidence of clock arms, points of clock faces and considered point events that occur at the same time and place” [21, p. 459]. From this citation we see that stating on one hand that “general theory of relativity can be thought only as the field theory. We would be unable to create it, holding the viewpoint that the real world consists of material points moving under affection of the forces of interaction” [25, p. 854], relativists factually confined themselves to the equivalence of coordinate systems transformation that is true only for material points and is inapplicable to the field processes. It is important to mark here that the initial assertion with which Einstein began to build his conception was just the asymmetry of Maxwell’s electrodynamics: “It is known that Maxwell’s electrodynamics in its today appearance applied to the moving bodies causes asymmetry that probably is not inherent in the phenomena. Recall, e.g., the electrodynamic interaction between a magnet and a wire with a current. The observed phenomenon depends here only on the relative motion of the wire and magnet, while conventionally two cases in which one either other body moves have to be separated. Indeed, if the magnet moved and wire rested, the electric field with some energy arises around the magnet and produces a current at the places where are the parts of wire. If the magnet rested and wire moved, around the magnet arises no electric field but in the wire there arises an electromotive force to which itself no energy relates but which – in the premised identity of relative motion in both cases of our interest – produces the electric currents of same value and direction as the electric field in the first case” [4, p. 7]. Actually, Maxwell, basing on Faraday’s experiments, pointed: “we have to strongly distinguish the electromagnetic forces moving the wire from the electromotive forces trying to produce the electric currents” [10, the footnote in the p. 57]. None the less, Einstein has chosen not the way to reveal the cause of such asymmetry – he at once turned the consideration into an idle fantasy: “The examples of such kind, as well as unsuccessful attempts to reveal the Earth’s motion with respect to ‘luminiferous medium’, bring us to a premise that not only in mechanics but in electrodynamics, too, no properties of phenomena correspond to the idea of absolute rest and even, moreover, – to the supposition that for all coordinate systems for which the equations of mechanics are true, the same electrodynamic and optical laws are true, as it has been already proven for the first-order values” [4, p. 7]. Now, understanding the difference between the motions of source and frame, we can better understand the difference between the motion of magnet and wire with respect to the magnet and can surely state that the difference is just caused by transformation of the force lines of source that take place when it moves and are absent when there moves the wire which in this case determines the reference frame. Anyway, the field of source has an energy, and Einstein is surely incorrect negating it. But this energy can be transmitted differently, so the case of moving magnet and resting wire and case of resting wire and moving magnet are different, they have to be modelled differently, which disables us to introduce the Einsteinian postulate of equivalent inertial frames and the postulate of constant speed of light in all inertial frames, as the frames are non-equivalent and the speed of light, when the frame moving with respect to aether, is not constant and, as (3.17) shows, depends on its speed. An obvious fact follows from it – it is incorrect to take the aether away from the physical conception. Just the interconnection of wave processes with the medium in which they occur causes the frames to be non-equivalent and brings the absolute frame resting with respect to the medium. It is surely convenient to introduce the absolute frame, as in this frame the speed of light is isotropic – this means, it is easier to build in it the etalons with which we can compare the processes in moving frames. Until the wave processes are interconnected with the medium, frames will be non-equivalent and Einsteinian postulates will be basically incorrect. We would underline again the basic difference between the study of field processes in mutually moving frames – and study of pattern of motion of material points in these frames. For those material points for which their material structure is out of our interest, the frames will be really equivalent. But if we think of the structure of these objects and, hence, of the interaction of molecules and atoms of which they consist, we pass to the field processes. So we come to the mutual non-equivalence of frames and related transformation of fields whose change of configuration unavoidably causes the transformation of geometric size of material bodies. This defines the pattern of transformation of classical models in passing to the speeds comparable with the speed of light. But this does not mean the transformation of time. As we showed, even in particular measurements, if the source and observer were mutually resting, the source will not change its frequency. This means, the time intervals will remain unchanged, which will keep unchanged the idea of time not only in the absolute meaning of philosophical generalisation but in the relative meaning of particular experimental practice. Though we have to mark here: possibly, there will take place also such processes which will cause the transformation of relative time in connection with the transformation of these processes dependently on the speed of frame with respect to the luminiferous medium. But, as it is done in experimental physics, we have to reveal these processes and to accept them invalid to measure the time intervals. The more that, as we showed, there exist processes able to keep their parameters in the change of speed of frame. And, as metrology engineers admit, the measurement with atomic clock is now most precise and quite satisfies both experimental physics and philosophical comprehension of physical processes. |
Contents: / 53 / 54 / 55 / 56 / 57 / 58 / 59 / 60 / 61 / 62 / 63 / 64 / 65 / 66 / 67 / 68 / 69 / 70 / 71 / 72 / 73 / 74 / 75 / 76 / 77 / 78 / 79 / 80 / 81 / 82 / 83 /