СЕЛФ |
60 |
| С.Б. Каравашкин и О.Н. Каравашкина | |
|
|
СЕЛФ |
60 |
| С.Б. Каравашкин и О.Н. Каравашкина | |
|
|
Вместе с тем, как мы выяснили в п. 3 работы, классическая теория принципиально иначе производит преобразования полевых процессов. В связи с наличием светоносной среды и учетом классической концепцией особенностей распространения световых волн в этой среде, в рамках классической концепции, как показано нами, существует четыре, а не две картины динамических полевых процессов: – картина, создаваемая источником, неподвижным относительно светоносной среды; в этой картине процессов отсутствует асимметрия эквифазных линий и описывается она системой уравнений (3.1), назовем его картиной F ; – отображение картины F , наблюдаемое движущимся относительно светоносной среды наблюдателем. В данной картине также отсутствует асимметрия эквифазных поверхностей, но все поверхности как единое целое смещаются во времени вместе со смещением системы отсчета относительно светоносной среды. Данная картина описывается системой уравнений (3.3); назовем ее картиной F' ; – картина эквифазных поверхностей, создаваемая движущимся относительно светоносной субстанции источником с точки зрения неподвижного относительно этой среды наблюдателя. Данная картина содержит асимметрию эквифазных поверхностей, которая зависит от скорости движения источника по отношению к среде. Данная картина описывается системой уравнений (3.15), и назовем мы ее для краткости картиной G ; – наконец, четвертая картина описывает отражение картины G движущимся относительно светоносной субстанции наблюдателем. Данная картина, как и картина G , содержит асимметрию эквифазных поверхностей, которая не зависит от скорости движения наблюдателя, но только зависит от скорости движения источника относительно среды. От картины G данная картина отличается изменением скорости пространственного смещения картины эквифазных поверхностей во времени в целом. Назовем мы ее картиной G' . Хотя классическая концепция
описывает четыре картины процессов, и все эти
картины процессов являются самостоятельными,
тем не менее мы не можем из любой картины
процесса перейти к любой картине. Физические
свойства светоносной субстанции существенно
ограничивают возможные трансформации картины
полей. В частности, невозможен переход F Описанные особенности можно представить систематически в виде графа допустимых преобразований, вид которого показан на рис. 4.7а.
|
а б Рис. 4.7. Схемы допустимых путей преобразования между картинами динамических процессов в поле с точки зрения классической физики (а) и с точки зрения релятивистской концепции (б); красными стрелками обозначены запрещенные переходы в классической концепции
|
Вид диаграммы четко определяется различием, которое выявляется классической физикой между движением источника и движением системы отсчета. В этом проявляется особенность ньютоновского разделения движений на относительные и абсолютные. Движение источника поля в этом смысле может быть только абсолютным и в зависимости от этого движения происходит трансформация картин процессов. Движение же системы отсчета всегда относительно, и потому это движение приводит только к смещению картин процессов как целого, сам же вид картин определяется состоянием движения источника относительно светоносной субстанции. Преобразование картин
процессов, реализуемое релятивистской
концепцией, также можно представить в виде
некоторого графа, вид которого показан на рис.
4.7б. Как мы видим, графы на рис. 4.7а и 4.7б
принципиально разнятся. Как показал анализ,
проведенный выше, релятивистская концепция по
сути реализует переход F Тем не менее, с точки зрения физики и на промежуточном этапе видна вся искусственность релятивистских преобразований. В частности, когда мы представляли проекцию распространения эквифазных поверхностей на диаграмме на рис. 4.2, Читатель мог обратить внимание, что красные маркеры, отображающие положение проекций эквифазных поверхностей, распространяются с разной скоростью в обе стороны от источника. В то же время, в рамках релятивистского формализма можно строго доказать, что скорость распространения этих маркеров в пространстве происходит с одинаковой скоростью, равной скорости света, что определяется не скоростью движения маркеров, а наклоном линии, вдоль которой они движутся в плоскости (x', ct') и этот наклон строго равен 45o . Действительно, на основе преобразований Лоренца (4.1) мы можем записать |
 |
(4.25) |
где Но вот то, что маркеры движутся с различной скоростью вдоль данной наклоненной плоскости событий, обусловлено тем, что законы преобразования временных интервалов различны вследствие материализации времени в преобразованиях Лоренца путем введения пространственного параметра x в уравнение для преобразования времени. Правда, последнее мало волновало и Эйнштейна, и последующих сторонников релятивизма. “Они играют в свои символы, а мы в Кавендише добываем неподдельные твердые факты природы” говорил по этому поводу Резерфорд [26, с. 541]. Для релятивистов “теория относительности являет собой прекрасный пример современного пути развития фундаментальной теории. Исходные гипотезы становятся все более абстрактными, все более далекими от ощущений. Но зато мы все ближе подходим к важнейшей цели науки – из наименьшего числа гипотез или аксиом логически получить дедуктивным путем максимум реальных результатов. При этом мысленный путь от аксиом к ощущаемым результатам становится все длиннее, все утонченнее” [27, с. 279]. Но не зря при этом Эйнштейн искал снисхождения себе на том пути, которым он шел: “и теоретика, занимающегося этим, не следует с упреком называть фантастом. Нет, лучше одобрить его фантазии, поскольку другого пути к цели для него вообще не существует (? – авт.). Это вовсе не беспредметные фантазии, а поиски логически простейших возможностей и их следствий. Этот призыв к снисхождению был необходим для того, чтобы слушатель или читатель проявил большую склонность с интересом следовать излагаемому ниже ходу развития идей” [27, с. 280]. В реальности путь Эйнштейна и последующих релятивистов заключался как раз в пренебрежении физической особенностью явлений в угоду математической красивости. Это отразилось, в частности, на том, что релятивизм пошел на нарушение законов преобразования картин волновых процессов в угоду красивости записи четырехмерного интервала и при этом полностью отторг физическую сущность процессов, оставив только урезанные математические формулы, оторванные от феноменологической базы, на которой были основаны их выводы. Действительно, когда Эйнштейн при выводе преобразований Лоренца записывает: “… относительно начала координат системы k луч света при измерении, произведенном в покоящейся системе, движется со скоростью V - v , вследствие чего |
| (4.26) |
[4, с. 15], он, сам того не желая, учитывает свойства взаимодействия световой волны с покоящейся светоносной средой, влияние которой отрицает. Точно так же, когда он записывает: “Пусть в момент времени tA из A выходит луч света, отражается в B в момент времени tB и возвращается назад в A в момент времени t'A . Принимая во внимание принцип постоянства скорости света, находим |
| (4.27) |
где rAB – длина движущегося стержня, измеренная в покоящейся системе” [4, с. 12], он тоже невольно для себя учитывает именно волновые свойства взаимодействия света со светоносной средой. При этом из выражений (4.27), взятых Эйнштейном из классической физики, не следует его вывод: “… не следует придавать абсолютного значения понятию одновременности. Два события, одновременные при наблюдении из одной координатной системы, уже не воспринимаются как одновременные при рассмотрении из системы, движущейся относительно данной системы” [4, с. 13]. Неодновременность возникает тогда, когда постулируется равенство времени, затраченное светом для прохождения путей от A к B и обратно независимо от состояния движения системы отсчета. Но именно к такому результату приводят релятивистские выражения (4.10) и (4.23), полученные путем асимметричного преобразования времени. Поэтому некорректно называть релятивистский подход следствием логической дедукции из закономерностей природы, как пытался представить это Эйнштейн в вышеприведенной цитате. “В случае дедуктивного вывода следствия содержатся в посылках в скрытом виде, и они должны быть извлечены из них в результате применения методов логического анализа” [28, с. 110]. В случае релятивизма посылкой были не общие закономерности природы, а абстрактная гипотеза о постоянстве скорости света во всех системах отсчета, не имеющая отражения в реальности и только отдаленно проявляющая похожесть на некоторые внешние проявления физических процессов. При этом данная похожесть столь неполная, что при малейшем уточнении появляющееся несоответствие порождает парадоксы и требует дальнейшей подмены физического содержания математическими символами, что и отражает весь путь развития релятивистской концепции. Базовый же постулат о постоянстве скорости света во всех системах отсчета как не был обоснован тогда, в момент своей формулировки в 1905 году, так не обоснован и до сих пор, а дальнейшее развитие релятивистской концепции привело к формальному отказу от этого постулата. Ведь если по мнению релятивистов постоянство скорости света согласно ОТО проявляется только локально, то в соседних локальных точках скорость света уже различна. Вместе с тем даже мысленные эксперименты, в которых используются системы отсчета, движущиеся с околосветовыми скоростями, никаким образом нельзя втиснуть в понятие локального, если время проведения любого эксперимента, умноженное на скорость света, сравнимо с размерами гравитирующих тел и тем более выходит за границы области однородного гравитационного потенциала. Эйнштейн прекрасно понимал, что далеко не всякое утверждение может служить базой физической концепции. Поэтому он с самого начала предпринимал попытки обоснования постулата, но в отсутствие прямых доказательств, он прибегал к стандартному способу искажения логики, пытаясь доказать посылку ее следствием. Действительно, когда
релятивисты доказывают справедливость
постулата, они это делают обычно двумя способами.
Первым способом пользовался Эйнштейн: “Пусть в момент
времени t = |
| (4.28) |
Преобразуем это уравнение с помощью записанных выше формул преобразования (аналогом которых в нашей статье является стандартная система уравнений Лоренца (4.1) – авт.); тогда получим |
| (4.29) |
Итак, рассматриваемая волна, наблюдаемая в движущейся системе, также является шаровой волной, распространяющейся со скоростью V ” [4, с. 16]. Второй способ доказательства основывался также на общей системе уравнений Лоренца. Идя этим путем, релятивисты на основе (4.1) находят дифференциалы координат и времени в обеих системах отсчета, принимая |
 |
(4.30) |
откуда путем деления первого равенства на второе получают |
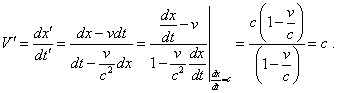 |
(4.31) |
Как видим, в обоих случаях использовались преобразования Лоренца в самой общей отвлеченной форме, и доказывается постоянство скорости света, на основе постулирования которого как раз и были получены преобразования Лоренца. Если же говорить о том, что есть на самом деле и что соответствует изученным свойствам природных явлений, то существует два описания процессов излучения/поглощения. Первое описывает испускание/поглощение и движение частиц. В этом случае скорость частицы, испущенной движущимся источником, будет в общем случае складываться со скоростью самого источника (естественно, если ее масса значительно меньше массы источника). Поэтому если мы попробуем описать для частицы интервалы времени в эйнштейновской модели, то для пути от A к B получим |
| (4.32) |
или |
| (4.33) |
Аналогично, для обратного пути от B к A , с учетом полностью упругого отражения от массивной преграды, получим |
| (4.34) |
или |
| (4.35) |
Выражения (4.33) и (4.35) показывают, что в случае суммирования скорости частицы со скоростью источника интервалы времени, за которые частица пролетает путь туда-обратно, с точки зрения неподвижного наблюдателя равны. Точно так же будут равны и интервалы времени в подвижной системе отсчета. Здесь следует отметить, что именно корпускулярное представление распространения света, завуалированное Эйнштейном в СТО отсутствием доопределения свойств света, связывает релятивистскую концепцию с фотонной концепцией, построенной на тех же гносеологических принципах отрицания физической реальности и подмены феноменологии процессов математической символикой, характерных для ТО. Вместе с тем, скорость частицы, измеренная неподвижным наблюдателем, на неподвижном интервале покажет суммирование скорости частицы со скоростью источника, что являлось бы откровенным противоречием исходному постулированию независимости скорости света от системы отсчета. И этот момент противоречия был критически важным для Эйнштейна – не доопределять свойства света, хотя в отсутствии эфира как светоносной среды корпускулярное представление света было бы единственно логичным следствием. Второй способ описания связан с процессами в среде. Основа данного подхода обусловлена тем, что эквифазная поверхность, излученная источником, распространяется в среде и подчиняется не законам движения источника, но законам передачи возмущения самой средой. Причем это могут быть и механические, и электрические, и гравитационные законы передачи возмущения. Но именно вследствие этой передачи возмущения от точки к точке возникает тот самый эффект независимости скорости распространения волны от скорости движения источника, обусловливающий постоянство скорости распространения волнового процесса относительно среды. Этот подход как раз и приводит классическую физику к решениям (4.27), которые позаимствованы у нее Эйнштейном с подменой следствий. Поэтому если мы изымем среду в любой ее форме или части свойств, то тем самым нарушим физику процесса передачи возмущения от точки к точке, поскольку при этом изымается основа для самой передачи возмущений. Нарушая же физику процесса, мы лишаем себя права вводить подобную независимость скорости света от характера движения источника, как “повисает” и сам физический процесс передачи возмущений от точки к точке, – что, собственно, и наблюдается в релятивистской концепции. Расширяя данный анализ на классический формализм, мы можем сделать однозначный вывод: причина того, что для описания материальных точек галилеевы системы эквивалентны, а для описания полевых процессов – нет, заложена в различии подходов к описанию частиц – сиречь, материальных точек с одной стороны и полей с другой стороны. Классическая концепция до сих пор не акцентировала внимание на этой особенности, что, безусловно, создавало определенные проблемы и препятствовало решению многих задач, как, кстати, послужило и причиной появления релятивистской концепции. Но для классической физики прояснение различия между преобразованием характеристик частиц и полей при переходе из одной инерциальной системы отсчета в другую не критично и неспособно уничтожить сам классический формализм до основания, поскольку классические преобразования не искажают плоскость событий. Это в данном случае является определяющим, поскольку при этом сохраняются основные свойства времени. В случае же релятивистского формализма, представленное нами уточнение физики процессов приводит к уничтожению всего его аппарата, ибо, начиная с постулатов, релятивистская концепция не только входит в противоречие с физикой процессов в динамических полях, но приводит к следствиям, полностью противоречащим и постановке задачи в самой релятивисткой концепции, и наблюдаемым явлениям. В результате всё обоснование релятивистов фактически сводится к тому, что “если скорость, в частности скорость света, принципиально невозможно измерить без произвольных допущений, то мы имеем право делать произвольные предположения и о скорости света” [29, с. 181]. Тем самым релятивисты только подчеркивают, что при формировании своей концепции некорректно проанализировали совокупность существующих экспериментальных методик, целью которых как раз и является отсеивание произвольных допущений при переходе от частных исследований к их обобщениям, – о чем, собственно и говорил И. Ньютон и на основе чего разделял понятия относительного и абсолютного. Потому у релятивистов и получается: “вопрос о том, реально лоренцово сокращение или нет, не имеет смысла. Сокращение не является реальным, поскольку оно не существует для наблюдателя, движущегося вместе с телом; однако оно реально, так как оно может быть принципиально доказано физическими средствами для наблюдателя, не движущегося вместе с телом” [30, с. 187]. Тем не менее в результате анализа классического и релятивистского подходов к проблеме описания полевых процессов в системах отсчета, мы должны констатировать, что существует два замкнутых математических формализма описания полевых процессов. Оба пути показывают формально замкнутую математическую логику, в рамках которой принципиально невозможно ни подтвердить, ни опровергнуть тот или иной математический аппарат. В частности, мы видим, что релятивистские переходы между F и G , хотя и являются некорректными с точки зрения феноменологии классической физики, вместе с тем математически строго переводят одно соотношение в другое и обратно. И это вполне ожидаемо, поскольку все преобразования, которые мы производили, например, с исходными уравнениями (4.2), были линейными, как линейными по x'a , y'a и t' были сами уравнения (4.2). Аналогично с (4.20) и (4.23). Поэтому полученные уравнения (4.10) и (4.23) нельзя рассматривать как подтверждение или опровержение релятивистской концепции. Эти решения лежат внутри того же релятивистского формализма, что и исходные выражения (4.2) и (4.20), а потому, будучи линейными по своим свойствам, естественно удовлетворяют всем свойствам, которым удовлетворяют и преобразования Лоренца. Также понятна и причина замкнутости релятивистского формализма. Она следует из самого графа. Ведь конечным преобразованием у релятивистов являются картины F и G. В обеих картинах, согласно расчетам, проведенным нами в п.3, скорость распространения света постоянна, а картины F'' и G'' принципиально искажены наклоном плоскости событий и в действительности являются промежуточным звеном между картинами F и G . Вследствие этого картины процессов F'' и G'' не обладают самостоятельной сущностью, как картины F' и G' классического формализма, поскольку в них нарушено условие наличия физического времени в системах отсчета. Переход у релятивистов в действительности осуществляется между F и G и здесь, если не принимать во внимание физику процессов, обуславливающую неправомерность самого перехода между F и G , в обеих картинах процессов скорость постоянна, что автоматически удовлетворяет введенному Эйнштейном постулату. Поэтому и невозможно вскрыть противоречия релятивистской концепции, оперируя зависимостями, заложенными в формализм концепции. Указанная невозможность аналогична тому, как бессмысленно, например, пытаться обосновать в геометрии равенство суммы углов треугольника 180o при помощи стандартной тригонометрии, поскольку сама тригонометрия основывается на данном равенстве и естественно будет подтверждать его справедливость. Только уйдя от условия равенства суммы углов треугольника 180o , можно ожидать доказательство или опровержение данного условия, что в свою очередь сводится к V постулату Евклида о параллельных прямых. Именно поэтому все попытки доказать V постулат в рамках формализма Евклидовой геометрии “не достигали намеченной цели, так как смысл проблемы заключался в освобождении евклидовой теории параллельных от специального постулата, и, таким образом, дело здесь было не в том, чтобы заменить V постулат другими утверждением, хотя бы оно и было весьма очевидным, а в том, чтобы доказать этот постулат, исходя из остальных постулатов геометрии” [31, с. 18]. Аналогично и с полученными нами решениями (4.10) и (4.23). Чтобы показать соответствие свойств полученных решений реальным свойствам пространства-времени, мало ввести исходные решения (4.2) и (4.20) в соответствие с условием наличия физического времени в обеих системах отсчета. Сам факт применения преобразований Лоренца предопределяет и направленность переходов в графе на рис. 4.7б. Чтобы проверить, какой из двух формализмов отражает действительность, нужно сверить эти формализмы с самой действительностью. Направление проверки вполне очевидно. Как мы видели, классический формализм не предусматривает трансформаций картины при переходе от неподвижной относительно светоносной субстанции системы отсчета к движущейся, в то время как эйнштейновская ТО всегда предполагает трансформацию картины при указанных переходах. Поэтому, исходя из построенных графов на рис. 4.7, проверке должна подлежать именно правомерность переходов от одной картины процессов к другой, и на основе того, какая из структур переходов отражает реальность, можно судить о правомерности того или иного формализма. Чтобы провести проверку качественно, мы должны базировать рассуждения на тех тезах, которые являются бесспорными для обеих концепций и не опираться на суждения, которые подлежат проверке или являются спорными. Первой такой тезой является неподвижная инерциальная система отсчета с неподвижным в ней источником света. Если мы с точки зрения классической физики предположим в качестве таковой систему отсчета, неподвижную относительно светоносной среды, то моделирующие уравнения, описывающие эквифазные поверхности для релятивистски неподвижной системы отсчета и классической неподвижной относительно светоносной субстанции системы отсчета, будут полностью идентичными. К тому же в рамках данной модели скорость распространения света в обеих концепциях тоже одинакова и изотропна. А следовательно, данная модель может служить базой для рассмотрения. Идя далее, мы должны ограничить рассмотрение процессов одной системой отсчета, поскольку противоречия, связанные с неодновременностью событий и вытекающих из этого следствий, на которых настаивает релятивистская концепция, возникают именно при переходах между системами отсчета. Но нас интересует именно представление эквифазных поверхностей с точки зрения движущейся системы отсчета, что, казалось бы, неминуемо должно приводить к появлению движущейся системы отсчета. Оказывается, не всегда в этом появляется необходимость. Отсутствие этой необходимости с точки зрения классической физики очевидно, поскольку в ее формализме само пространство и тем более время не трансформируется; могут трансформироваться только наши меры, что не адекватно трансформации пространства-времени. Поэтому мы вполне можем наблюдать процессы в движущихся системах отсчета из неподвижной системы. Но и релятивизм вынужден признавать подобную возможность наблюдения процессов и трансформаций из неподвижной системы отсчета. В частности, вспомним вышеприведенную цитату Эйнштейна о реальности трансформаций пространства-времени: “Сокращение не является реальным, поскольку оно не существует для наблюдателя, движущегося вместе с телом; однако оно реально, так как оно может быть принципиально доказано физическими средствами для наблюдателя, не движущегося вместе с телом” [30, с. 187]. Исходя из этого, если в подвижной системе отсчета существует асимметричная трансформация эквифазных поверхностей, она должна быть наблюдаема из неподвижной системы отсчета. Особенно, если мы будем наблюдать за тем, как происходит отображение информации движущимся фиксирующим устройством с точки зрения неподвижной системы отсчета. В качестве такого регистратора, широко используемого в научной экспериментальной практике, может быть использована фотографическая пластина, которая одновременно регистрирует события в определенной плоскости независимо протекающими химическими реакциями. Чтобы не вдаваться в риторический спор, одновременно ли протекают реакции с точки зрения подвижного наблюдателя, мы будем наблюдать данные реакции с точки зрения неподвижного наблюдателя, учитывая то свойство релятивистской концепции, что она вынуждена признавать реальность уже записанного свидетельства. Так, в частности, если мы зафиксируем картину эквифазных поверхностей в неподвижной системе отсчета неподвижной фотопластиной и передадим это изображение подвижному наблюдателю, он не может рассматривать зафиксированное на ней изображение с точки зрения релятивистской неодновременности. Изображение для него является фактом, как является для релятивистов фактом инвариантность фазы волны независимо от системы отсчета: “фаза должна быть инвариантна” [23, с. 36]. С тем же успехом мы можем зафиксировать изображение на движущуюся фотопластину и предъявить ее движущемуся наблюдателю. И это также будет для последнего фактом. Во втором случае зафиксированное пластиной изображение должно быть идентично изображению, полученному самим движущимся наблюдателем, если скорость и направление движения пластины совпадают со скоростью и направлением движения этого наблюдателя. Таким образом, исследуя процесс фиксации эквифазных поверхностей с точки зрения неподвижного наблюдателя, мы, обходя необходимость перехода в подвижную систему отсчета, можем определить принципиальный для нас факт: трансформируются ли эквифазные поверхности в движущейся системе отсчета или нет, и как следствие выявить физическую справедливость одной или другой концепции. Чтобы реализовать данное исследование наиболее корректным способом, будем исходить из бесспорного в данном случае факта, что эквифазные поверхности в выбранной нами неподвижной системе отсчета имеют вид концентрических колец. А следовательно, если мы установим на пути распространения света фиксаторы, расположенные в форме колец, то они будут отображать и геометрию эквифазных поверхностей. Исходя из этого, возьмем некоторый цилиндрический импульсный источник света и концентрически расположим вокруг него конические полупрозрачные отражатели, позволяющие части светового сигнала проходить на следующие отражатели, а часть световой волны отклоняющие в направлении, перпендикулярном направлению распространения света. При этом размер конических отражателей выберем таким образом, чтобы расстояния между кольцами были равны произведению скорости распространения света на период между импульсами. Несложно убедиться, что данная схема строго моделирует мгновенную картину эквифазных поверхностей. Причем конические отражатели являются далеко не единственным решением задачи. На их месте можно было бы установить датчики, фиксирующие фазу волны (или в случае нашего импульсного источника – фиксировать световой импульс) и испускающие световой импульс на фотопластинку в момент фиксации фазы. Результат был бы тем же. Идя далее, разместим регистрирующую фотопластину таким образом, чтобы она двигалась с некоторой скоростью над вышеуказанной системой конических отражателей на определенной высоте h , как это показано на рис. 4.8. |
Рис. 4.8. Схема, моделирующая картину эквифазных поверхностей в неподвижной системе отсчета
|
Из построения на рис. 4.8 видно, что все лучи, отраженные коническими зеркалами, будут достигать фотопластины одновременно – конечно, с точки зрения неподвижного наблюдателя, что для рассматриваемой схемы вполне достаточно. Ведь достигая фотопластины, лучи запускают химические реакции, оставляя на последней не относительное, а абсолютное изображение. При этом независимо от того, рассматривает ли подвижный наблюдатель одновременность достижения светом пластины или нет, он может видеть только результат химической реакции, которая не зависит от релятивистской неодновременности, ибо проявляется фактом почернения кристалликов фотоэмульсии в определенных местах фотопластины. Также места почернения не будут зависеть от того, изменился ли продольный размер фотопластины. В случае подобного сжатия, этот размер должен измениться для всех участков и способен только перевести окружности в эллипсы, но перевести концентрические окружности в асимметрично расположенные не может. Вместе с тем, именно этого следует ожидать, если релятивистский подход справедлив, и этого не следует ожидать, если справедливо моделирование классической физики. Поэтому проведем моделирование процессов с точки зрения неподвижного наблюдателя и определим, проявляется асимметричная трансформация или нет. Результаты показаны на рис. 4.9. |
Рис. 4.9. Моделирование процессов фиксации эквифазных поверхностей коническими отражателями с точки зрения неподвижной системы отсчета при скорости движения фотопластинки v = 0,8 c
|
Диаграмма показывает, что независимая регистрация дает картину нетрансформированных эквифазных поверхностей, а следовательно, справедливо классическое представление. Здесь следует особо отметить, что уменьшая высоту h до нуля, мы переходим от опосредованной к непосредственной фиксации эквифазных поверхностей и на всем пути уменьшения h картина будет оставаться неизменной. Следовательно, в пределе, при непосредственной фиксации эквифазных поверхностей также будет наблюдаться неискаженная картина, подтверждающая справедливость классического формализма. Данная картина будет той реальностью, которая независима от наблюдателя. Так, если, предположим, подвижный наблюдатель будет пытаться определять взаимное положение колец своими мерами длины, в предположении их трансформированности, то он не выявит асимметрии колец, которой и нет, в то время как согласно релятивистской концепции он данную асимметрию обязан выявить. Можно предположить, что сторонники эйнштейновской теории относительности попытаются представить отпечатки не на горизонтальной плоскости событий, соответствующей одновременной фиксации эквифазных поверхностей, а на наклоненной релятивистской плоскости событий. Для того, чтобы предупредить эти попытки втиснуть неодновременность в физику, достаточно вспомнить правило формирования эквифазных поверхностей, согласно которому каждая эквифазная поверхность излучается источником на один период раньше вложенной эквифазной поверхности. Следовательно, если в световом импульсе дополнительно будет передаваться изображение кода времени излучения, то на всех концентрических поверхностях, зафиксированных пластинкой, время регистрации будет убывать в четком соответствии с периодом излучения. Эти данные могут быть использованы и для синхронизации физического времени в системе отсчета подвижного наблюдателя, и могут показывать одновременность регистрации. Кстати, если по примеру релятивистов пренебрегать особенностями физических процессов, то можно на основе зафиксированных данных на отпечатках эквифазных поверхностей построить другую поверхность одновременности, которая будет расходиться конусом от центральных эквифазных поверхностей к периферийным. Это уже не будет наклоненная плоскость, но на основе этого “конуса неодновременности” также можно построить некоторое внутренне замкнутое математическое ядро. Однако это ядро будет справедливо исключительно в тех рамках, в которых оно было построено, и будет ограничено закономерностями измерительной схемы, которой было обосновано. Изменится схема, изменятся условия измерения, и математическое ядро начнет давать парадоксальные результаты. Так, в рассматриваемом случае маркированных отпечатков эквифазных колец, если мы установим, как описано ранее, вместо конических отражателей датчики фазы с синхронными излучателями, то учитывая возможность синхронизации часов, соединенных с каждым из этих датчиков в неподвижной системе отсчета, мы получим уже иную маркировку эквифазных поверхностей на пластине. Эта маркировка будет определять горизонтальную плоскость событий, поскольку все маркеры сработают одновременно и свет от них с точки зрения неподвижной системы отсчета достигнет пластины одновременно – а следовательно, и момент фиксации будет один и тот же. При этом сам факт, что некоторой области подвижной системы отсчета может быть задано физическое время из другой системы отсчета и именно с помощью световых лучей, говорит о том, что релятивистская неодновременность в действительности не является физическим явлением, но является одним из первых парадоксов, с которыми столкнулся Эйнштейн и, не желая отказываться от абстрактного математического ядра, необоснованно перевел его в разряд физических явлений вместо того, чтобы уточнить постановку задачи, немедленно показавшую Эйнштейну парадоксальный характер наклона плоскости событий, как и то, что неодновременность ни в коем случае не является причиной, но является следствием постулирования постоянства скорости света во всех системах отсчета. Поэтому можно с уверенностью говорить, что причина неодновременности, как и другие парадоксы эйнштейновской ТО, заключена не в неопределенности физических явлений, а в том, что частность была неправомерно обобщена путем обобщения математических выражений, построенных на частном эффекте или схеме измерения. Особенность же математического аппарата в общем понимании возможностей этого научного инструмента заключена в том, что он значительно шире по своим возможностям, чем это необходимо для физического описания явлений природы. Поэтому он способен генерировать множество вариантов, тем более, если он прилагается к неполной или намеренно ограничиваемой в своей формулировке феноменологической базе. Так, например, пренебрегая условием строгой положительности массы, мы с точки зрения математики можем во втором законе Ньютона сделать массу тела отрицательной и даже комплексной, и это нисколько не будет противоречить операциям, производимым над формулами. При этом мы можем сформировать внутренне замкнутую математическую концепцию, которая к тому же отдельными результатами будет совпадать с наблюдаемыми явлениями. Точно так же мы можем принять частоту процесса отрицательной и тоже будем получать математически согласующиеся между собой результаты, и подобных примеров можно привести много, как и разрабатывается сейчас множество вариантов “теорий всего”, в основу которых закладывается не максимально полная информация о явлениях, но некоторая часть, удобная для формирования непротиворечивой математики. Общим для всех этих концепций является то, что в каждом случае игнорируется то или иное свойство физического явления, как, например, игнорируется релятивистами однонаправленность времени; или, как мы видели выше, снимается принципиальное ограничение возможных переходов между картинами полевых процессов, допускающее переход от картины F к картине G . При этом зачастую, если подходить исключительно с точки зрения математики, формально ничего не мешает связать некорректные с точки зрения физики переходы, как и ввести 32-мерное физическое пространство, искривить время, наклонить ось событий и т.д. Но наряду с безупречной математической связностью, в подобной концепции появятся и парадоксальные результаты, связанные со столкновением полученных абстрактным манером результатов с опытом, которые и порождают парадоксы, как например в случае отрицательной массы тело будет двигаться навстречу воздействующей силе. Или как в теории Эйнштейна: “закон параллелограмма скоростей в нашей теории верен только в первом приближении” [4, с. 20]. А если быть точным, то именно в том приближении, когда можно пренебречь релятивистскими множителями, перейдя к формализму классической физики. Также мы будем получать, что гравитационное взаимодействие может быть не только притягивающим, но и отталкивающим, как придем к возможности отрицательной кинетической энергии тела. При этом можно пытаться давать различные трактовки появляющимся парадоксам, но на следующем же шаге данные трактовки будут оказываться ложными и нужно будет искать для новых проявлений новые трактовки или снова пренебрегать свойствами изучаемых явлений, потому что новые трактовки будут противоречить предыдущим, поскольку парадоксы как раз и возникают когда трактовка неспособна обосновать весь комплекс наблюдаемых явлений, а объясняя только часть наблюдаемых свойств, неминуемо входит в противоречие с остальными проявлениями. Тем более это характерно, когда наблюдаемые физические свойства втискиваются в рамки некоторого абстрактного математического описания или постулата. Характерным примером тому может служить понятие звездной аберрации. В своей основе это расхождение между углом, под которым находится звезда, и углом наклона квадранта ли, секстанта ли, телескопа ли. Да, это основные астрономические приборы, используемые человечеством для наблюдения звезд, но все они построены на общем принципе совмещения визиров, который и приводит к появлению аберрации. И это важная особенность, отделяющая понятие физической основы аберрации как паразитного явления, возникающего при наблюдении определенным методом, от физических свойств астрономических объектов, и в частности от свойств пространства. Но со временем эта особенность явления была опущена, и уже в энциклопедическом словаре мы читаем: “аберрация света (в астрономии) – изменение видимого положения светила на небесной сфере, обусловленное конечностью скорости света и движением наблюдателя вследствие вращения Земли (суточная аберрация света), обращением Земли вокруг Солнца (годичная аберрация света) и перемещением Солнечной системы в пространстве (вековая аберрация света)” [32, с. 9]. Таким образом, причина появления звездной аберрации фактически заменилась условием, определяющим закономерность ее изменения. При этом нельзя отрицать, что аберрация не связана со скоростью движения наблюдателя. Причиной возникновения аберрации является не движение, но необходимость совмещения визиров. Она возникает из необходимости совмещения меток, разнесенных на расстояние друг от друга, но само расстояние между метками при математическом описании сокращается и остается зависимость от скорости движения тела, т.е. вторичная причина, которая без первичной причины проявляться не будет. В результате указанной неточности в определении, в концепции релятивистов это преобразуется к тому, что звездная аберрация уже является неотъемлемой составляющей искажения пространства-времени и мы, производя переход между штрихованными и нештрихованными полярными углами, фактически использовали релятивистскую формулу аберрации (4.15), поскольку угловые меры в релятивистской концепции искажены именно вследствие взаимного движения систем отсчета, а не вследствие необходимости совмещения визиров. В действительности данная формула никакого отношения к физическим явлениям в пространстве не имеет, поскольку, как уже сказано, аберрация является исключительно инструментальной погрешностью, и если будет использован метод угловых измерений без совмещения визиров, но путем, например, одновременной стереосъемки двух звезд, угол одной из которых задан или определен предварительно, то аберрация не появится, поскольку до этого будет удалена причина ее появления. Вместе с тем в релятивистской концепции аберрация сохранится, поскольку ее физическая суть отделена от математического аппарата, и уже определяется не инструментальной методикой измерения, а некоторыми физическими явлениями, отделенными от нашего измерения и вообще от нашего наблюдения. Как следствие возникают парадоксы типа деформации эквифазных поверхностей углом вперед, который мы показали на рис. 4.3 и 4.5. Проведенное исследование показывает, что замкнутость математического ядра не является сама по себе подтверждением корректности физической концепции. Для того, чтобы физическая концепция правильно отражала явления природы, она должна содержать полную информацию в базовых принципах, на которой математическое ядро формируется. И эти принципы должны быть досконально проверенны путем экспериментального изучения явлений природы. Именно полный и корректный учет базовых свойств изучаемых явлений может гарантировать и корректность математического описания с точки зрения ассоциативности этого описания физике явлений. Исходя из этого, интересно проанализировать вопрос о геометризации физических явлений, которая была осуществлена релятивизмом на основе объединения пространственных и временных характеристик описания физических процессов, поскольку здесь мы тоже столкнемся с некоторым формально замкнутым математическим ядром и неассоциативной базой, на основе которой данное ядро было сформировано. |
Содержание: / 53 / 54 / 55 / 56 / 57 / 58 / 59 / 60 / 61 / 62 / 63 / 64 / 65 / 66 / 67 / 68 / 69 / 70 / 71 / 72 / 73 / 74 / 75 / 76 / 77 / 78 / 79 / 80 / 81 / 82 / 83 /